模函數

解析函數的許多經典理論如整函數理論中的皮卡定理、正規族理論中的一些判定定理，都可藉助模函數的性質來證明。

如圖1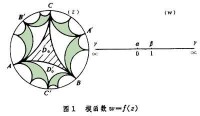,在z平面中取單位圓在其周界上按反時針向依次任取三點A，B，C,並作一圓弧三角形ABC，其每邊均與正交，構成一區域D0(圖中斜線區)。在w平面中實軸上取定三點,,。由共形映射的黎曼定理，存在一單葉解析函數,把映到w 的上半平面，並使A，B，C分別映到α，β，у。根據對稱性原理,可解析開拓到圓弧三角形Dó中，這裡Dó是關於AB 弧的對稱反演區域(C點反演成圓周上另一點C┡),而函數值則取在w 的下半平面，此下半平面與原上半平面沿線段相粘連。同理,又可分別解析開拓到D0的關於CA弧和BC弧的對稱圓弧三角形中，其函數值也在w 的下半平面中，它們分別與上半平面沿半直線 和 相粘連。這樣，得到了中的一圓弧六邊形區域,在其中解析，取值於整個w 平面中如上粘連的一個上半平面和三個下半平面。再以此六邊形的各邊進行反演，則又可再次解析開拓到中邊數更多的圓弧形區域中(仍在內),取值又回到w 的上半平面，並與上面已取得的下半平面分別沿，,уα之一相粘連。如此無限繼續下去，則就開拓成為整個內的解析函數，其所取之值在w平面上形成一無限層的黎曼曲面。稱為模函數。其反函數是整個w平面除0，1，外的多值解析函數，或者可說成是上述黎曼曲面上的單值解析函數。

模函數單值解析於內，顯然不取值0，1,,且當z從單位圓內部以任意方式趨於其周界上一點時，不可能有確定的極限值，因此是其自然邊界，即它不可能再向之外進行解析開拓。

也可用一分式線性變換,,把z變到t平面的上半平面，使A,B,C分別變成實軸的α,b以及，而0變成區域墹 0（圖2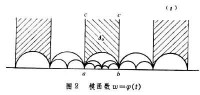），當關於其一邊界圓弧作對稱反演時，相應地墹 0也關於其相應邊作對稱反演。

設的反函數為，則

就把t的上半平面映成w平面的上述黎曼曲面。也稱為模函數，其性質本質上與ƒ(z)相類似。

如果把構成模函數過程中所作的種種關於圓弧的反演變換記為，,…，則對於任何，與互為共軛。因此，對任何兩個,，恆有，即當z經過兩次這類反演后，其函數值ƒ(z)不變。如果把偶數個這種反演及其逆作為元素，它們生成一變換群G，則當z經G任一元變換后，函數值ƒ(z)不變。稱G為模函數的不變群，也稱ƒ(z)為關於群G 的自守函數（見橢圓函數）。