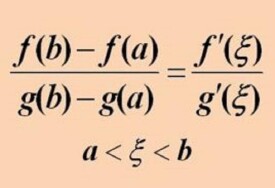柯西中值定理
微分學的基本定理之一
柯西中值定理是拉格朗日中值定理的推廣,是微分學的基本定理之一。其幾何意義為,用參數方程表示的曲線上至少有一點,它的切線平行於兩端點所在的弦。該定理可以視作在參數方程下拉格朗日中值定理的表達形式。
柯西中值定理粗略地表明,對於兩個端點之間的給定平面弧,至少有一個點,弧的切線通過其端點平行於切線。
柯西(Cauchy,Augustin Louis 1789-1857),出生於巴黎,他的父親路易·弗朗索瓦·柯西是法國波旁王朝的官員,在法國動蕩的政治漩渦中一直擔任公職。由於家庭的原因,柯西本人屬於擁護波旁王朝的正統派,是一位虔誠的天主教徒。並且在數學領域,有很高的建樹和造詣。很多數學的定理和公式也都以他的名字來稱呼,如柯西不等式、柯西積分公式。
⑴在閉區間上連續;
⑵在開區間內可導;
(3)對任意的;
那麼在 內至少有一點,使得成立.
可構造輔助函數在上連續,在內可導,且有
由羅爾定理可知,存在,使得,即又,所以有
此外,在柯西中值定理中,若取時,則其結論形式和拉格朗日中值定理的結論形式相同。
因此,拉格朗日中值定理為柯西中值定理的一個特例;反之,柯西中值定理可看作是拉格朗日中值定理的推廣。
若令,這個形式可理解為參數方程,而則是連接參數曲線兩端點弦的斜率,表示曲線上某點處切線的斜率,在定理的條件下,結論可理解如下:用參數方程表示的曲線上至少有一點,在這一點處的切線平行於連接兩個端點的弦。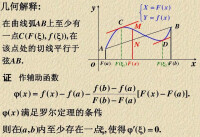

柯西中值定理
值得注意的是,雖然用參數方程表示的曲線上至少有一點,它的切線平行於兩端點所在的弦。
但柯西定理不能表明在任何情況下不同的兩點和都存在切線,因為可能存在一些c值使,換句話說取某個值時位於曲線的駐點;在這些點處,曲線根本沒有切線。下面是這種情形的一個例子
在區間[−1,1]上,曲線由(−1,0)到(1,0),卻並無一個水平切線;然而它有一個駐點(實際上是一個尖點)
柯西中值定理可以用來證明洛必達法則,拉格朗日中值定理是柯西中值定理當時的特殊情況。
柯西中值定理最主要的應用是證明帶有拉格朗日余項的階泰勒公式,只要反覆使用柯西中值定理多次就能證明,下面以為例說明。
例1設在內二次可微,證明:任意的,在之間存在,使
這就是函數在點鄰域內的一階泰勒公式。
證明:令利用在兩次應用到柯西中值定理后可以得到:
命題得證。
柯西中值定理的一個最重要的應用就是可以推導計算待定型的極限最有效的方法——洛必達法則。
洛必達法則是求兩個無窮小量或兩個無窮大量的比的極限。在滿足一定條件下可以化成兩個函數的導數的比值極限,這樣就有可能使得原待定型變成簡便而有效的求非待定型極限的問題。
我們得出下面這個定理(洛必達法則):
⑴兩個函數和在開區間可微,並且在這個開區間上,的導數不等於0;
⑵存在極限(或),其中A為一個有限的常數。則在以下情況下:(或者和)。那麼就有:(或)。在區間的另一個端點也存在類似的結果。這個定理就稱之為洛必達法則,能有效地應用於待定型的極限計算。
柯西中值定理在不等式的證明也有廣泛應用,關鍵是和要選得恰當。
例3.試證明當時,(引用文內原題,解法重新作出)。
證明:設則在區間上滿足柯西中值定理條件,所以存在,使,
即
結論得證。
中值點的存在性的證明是柯西中值定理最典型的應用之一。
例4設,函數在區間上連續,在內可導,則存在,使得證明:設,,顯然在上滿足柯西中值定理的條件,於是存在,使得
即存在,使得,即可得結論。
柯西(Cauchy)中值定理是微分中值定理的三大定理之一,它比羅爾(Rolle)定理與拉格朗日(Lagrange)中值定理更具一般性,也具有更廣泛的應用性,但大多高等數學的教材中僅介紹了柯西中值定理及其證明,對該定理的應用涉及較少,不利於學生對該定理的理解併發揮其應用價值。下面介紹一下利用柯西中值定理在求極限中的應用。
例:求極限
解:①當時,故②當時,令,
則與在上滿足柯西中值定理的條件,故存在,使得即故從而故又因為,所以,所以。綜合1、2,得:說明:柯西中值定理常用來求含形式的極限問題。