斐波那契法
一維搜索的區間消去法
斐波那契法(Fibonacci method),又稱Fibonacci法、斐波那契分數法,是一種一維搜索的區間消去法。這種方法與0.618法(黃金分割法)類似,也是用於單峰函數,在計算過程中,也是第1次迭代需要計算兩個迭代點,以後每次迭代只需新算一點,另一點取自上次迭代。斐波那契法與0.618法的主要區別在於:探索區間長度的縮短率不是採用黃金分割數,而是採用斐波那契數,計算函數值的次數n也是已知的。
義大利數學家斐波那契,提出了一個著名的“兔子數列”,該數列從第3個數起,後面的每個數都是它前面那兩個數的和。如果把斐波那契數列的任何一項除以前一項,將會得到一個比值極限約為0.618,俗稱黃金分割點,因此斐波納契數列又稱黃金分割數列,用數列{Fn}表示,則有:
這個級數與大自然植物的關係極為密切。幾乎所有花朵的花瓣數都來自這個級數中的一項數字:菠蘿表皮方塊形鱗苞形成兩組旋向相反的螺線,它們的條數必須是這個級數中緊鄰的兩個數字(如左旋8行,右旋13行);還有向日葵花盤等。直到最近的1993年,人們才對這個古老而重要的級數給出真正滿意的解釋:此級數中任何相鄰的兩個數,次第相除,其比率都最為接近0.618034……這個值,它的極限就是所謂的"黃金分割數"。斐波那契數列在許多科技領域都得到了應用。
對閉區間上的單峰函數f(t),按相鄰兩斐波那契數之比,使用對稱規則進行搜索的方法。其特點是:逐步縮短所考察的區間,以盡量少的函數求值次數,達到預定的某一縮短率。設{F}是斐波那契數列,對於區間[0,1],確定搜索次數n,則選擇兩點:
比較f(t)和f(t),消去其中較小值所在的一段區間;在縮短后的搜索區間上,再作第二步迭代;如此繼續迭代下去,共做n次迭代,搜索區間長度縮短為(使小於給定值)。1953年,美國數學家基弗(Kiefer,J.C.)首先研究用斐波那契數搜索一維函數f(t)的局部最大值。
Fibonacci法計算步驟如下:
(1) 給定初始區間 和最終長度L。求計算函數值的次數n,使,辨別常數,計算試探點 和,計算函數值 和;
(2) 若,則轉步驟(3);若,則轉步驟(4);
(3) 令,計算試點:
若,則轉步驟(6);否則,計算函數值,轉步驟(5);
(4) 令,計算試點:
若,則轉步驟(6);否則,計算函數值,轉步驟(5);
(5) 置,轉至步驟(2);
(6) 令,計算和;若,則令;若,則令。停止計算,極小點含於。
斐波那契法的流程圖如圖1所示。
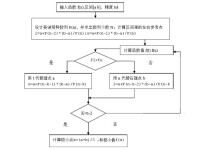
圖1
斐波那契法有如下應用領域:
(2)從運籌學的斐波那契法來論述波浪理論,也可以從斐波那契法的最優分划點來掌握波浪理論中的最佳投資。
