t分佈
t分佈
在概率論和統計學中,學生t-分佈(t-distribution),可簡稱為t分佈,用於根據小樣本來估計呈正態分佈且方差未知的總體的均值。如果總體方差已知(例如在樣本數量足夠多時),則應該用正態分佈來估計總體均值。
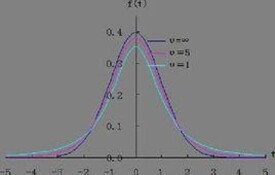
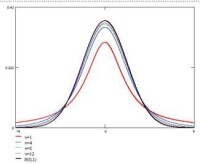
t分佈曲線形態與n(確切地說與自由度df)大小有關。與標準正態分佈曲線相比,自由度df越小,t分佈曲線愈平坦,曲線中間愈低,曲線雙側尾部翹得愈高;自由度df愈大,t分佈曲線愈接近正態分佈曲線,當自由度df=∞時,t分佈曲線為標準正態分佈曲線。
在概率論和統計學中,學生t-分佈(Student'st-distribution)經常應用在對呈正態分佈的總體的均值進行估計。它是對兩個樣本均值差異進行顯著性測試的學生t測定的基礎。t檢定改進了Z檢定(en:Z-test),不論樣本數量大或小皆可應用。在樣本數量大(超過120等)時,可以應用Z檢定,但Z檢定用在小的樣本會產生很大的誤差,因此樣本很小的情況下得改用學生t檢定。在數據有三組以上時,因為誤差無法壓低,此時可以用變異數分析代替學生t檢定。
當母群體的標準差是未知的但卻又需要估計時,我們可以運用學生t-分佈。
學生t-分佈可簡稱為t分佈。其推導由威廉·戈塞於1908年首先發表,當時他還在都柏林的健力士釀酒廠工作。因為不能以他本人的名義發表,所以論文使用了學生(Student)這一筆名。之後t檢驗以及相關理論經由羅納德·費雪的工作發揚光大,而正是他將此分佈稱為學生分佈。
由於在實際工作中,往往σ是未知的,常用s作為σ的估計值,為了與u變換區別,稱為t變換,統計量t 值的分佈稱為t分佈。
假設X服從標準正態分佈N(0,1),Y服從分佈,那麼的分佈稱為自由度為n的t分佈,記為。
分佈密度函數,
t分佈
t分佈
正態分佈(normal distribution)是數理統計中的一種重要的理論分佈,是許多統計方法的理論基礎。正態分佈有兩個參數,μ和σ,決定了正態分佈的位置和形態。為了應用方便,常將一般的正態變數X通過u變換[(X-μ)/σ]轉化成標準正態變數u,以使原來各種形態的正態分佈都轉換為,的標準正態分佈(standard normal distribution),亦稱u分佈。
根據中心極限定理,通過上述的抽樣模擬試驗表明,在正態分佈總體中以固定n,抽取若干個樣本時,樣本均數的分佈仍服從正態分佈,即 。所以,對樣本均數的分佈進行u變換,也可變換為標準正態分佈N (0,1)。
1.以0為中心,左右對稱的單峰分佈;
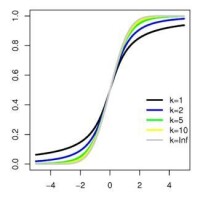
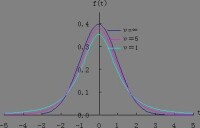
2.t分佈是一簇曲線,其形態變化與n(確切地說與自由度df)大小有關。自由度df越小,t分佈曲線越低平;自由度df越大,t分佈曲線越接近標準正態分佈(u分佈)曲線,如圖:
t分佈
3.隨著自由度逐漸增大,t分佈逐漸接近標準正態分佈。
對應於每一個自由度df,就有一條t分佈曲線,每條曲線都有其曲線下統計量t的分佈規律,計算較複雜。
學生的t分佈(或也t分佈) ,在概率統計中,在置信區間估計、顯著性檢驗等問題的計算中發揮重要作用。
t分佈情況出現時(如在幾乎所有實際的統計工作)的總體標準偏差是未知的,並要從數據估算。教科書問題的處理標準偏差,因為如果它被稱為是兩類:
( 1 )那些在該樣本規模是如此之大的一個可處理的數據為基礎估計的差異,就好像它是一定的;
( 2 )這些說明數學推理,在其中的問題,估計標準偏差是暫時忽略的,因為這不是一點,這是作者或導師當時的解釋。
假設數量A在當T呈t-分佈(T的自由度為n−1)滿足這與是相同的。A是這個概率分佈的第95個百分點。
那麼
等介於
因此μ的90%置信區間為:。
下表列出了自由度為1-30以及80、100、120等t-分佈的單側和雙側區間值。例如,當樣本數量時,則自由度df=4,我們就可以查找表中以4開頭的行。該行第5列值為2.132,對應的單側值為95%(雙側值為90%)。這也就是說,T小於2.132的概率為95%(即單側),記為;同時,T值介於-2.132和2.132之間的概率為90%(即雙側),記為。
這是根據分佈的對稱性計算得到的。
因此,
注意 關於表格的最後一行的值:自由度為無限大(n=120)的t-分佈和正態分佈等價。
| 單側 | 75% | 80% | 85% | 90% | 95% | 97.5% | 99% | 99.5% | 99.75% | 99.9% | 99.95% |
| 雙側 | 50% | 60% | 70% | 80% | 90% | 95% | 98% | 99% | 99.5% | 99.8% | 99.9% |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0.816 | 1.061 | 1.386 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.09 | 22.33 | 31.60 |
| 3 | 0.765 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | 0.741 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | 0.727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0.718 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | 0.700 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | 0.694 | 0.870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0.689 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0.687 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.104 | 3.485 | 3.767 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0.679 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 120 | 0.677 | 0.845 | 1.041 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 2.860 | 3.160 | 3.373 |
| 無窮大 | 0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.090 | 3.291 |