項目關鍵路徑

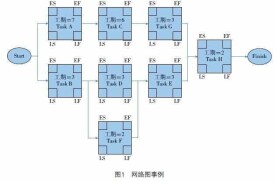
項鍵徑網路圖，雷頓-蘭司(- )( )杜邦司沃( )提，化廠維護項程排。適業且必須按完項。鍵線態系統，隨項展斷，該采單估計，視確。

）畫網路圖，節標件，箭業。整項整概觀。習慣項始左終止右。

）箭標項業持續（）

3）從左面開始，計算每項作業的最早結束時間（EF）。該時間等於最早可能的開始時間（ES）加上該作業的持續時間。

4）當所有的計算都完成時，最後算出的時間就是完成整個項目所需要的時間。

5）從右邊開始，根據整個項目的持續時間決定每項作業的最遲結束時間（LF）。

6）最遲結束時間減去作業的持續時間得到最遲開始時間（LS）。

7）每項作業的最遲結束時間與最早結束時間，或者最遲開始時間與最早開始時間的差額就是該作業的時差。

8）如果某作業的時差為零，那麼該作業就在關鍵路線上。

9）項目的關聯路線就是所有作業的時差為零的路線。

對於一個項目而言，只有項目網路中最長的或耗時最多的活動完成之後，項目才能結束，這條最長的活動路線就叫關鍵路徑（Critical Path），組成關鍵路徑的活動稱為關鍵活動。其通常做法是：

1）將項目中的各項活動視為有一個時間屬性的結點，從項目起點到終點進行排列；

2）用有方向的線段標出各結點的緊前活動和緊后活動的關係，使之成為一個有方向的網路圖；

3）用正推法和逆推法計算出各個活動的最早開始時間，最晚開始時間，最早完工時間和最遲完工時間，並計算出各個活動的時差；

4）找出所有時差為零或者為負數的活動所組成的路線，即為關鍵路徑；

5）識別出准關鍵路徑，為網路優化提供約束條件；

它具有以下特點：

1）關鍵路徑上的活動持續時間決定了項目的工期，關鍵路徑上所有活動的持續時間總和就是項目的工期。

2）關鍵路徑上的任何一個活動都是關鍵活動，其中任何一個活動的延遲都會導致整個項目完工時間的延遲。

3）關鍵路徑上的耗時是可以完工的最短時間量，若縮短關鍵路徑的總耗時，會縮短項目工期；反之，則會延長整個項目的總工期。但是如果縮短非關鍵路徑上的各個活動所需要的時間，也不至於影響工程的完工時間。

4）關鍵路徑上活動是總時差最小的活動，改變其中某個活動的耗時，可能使關鍵路徑發生變化。

5）可以存在多條關鍵路徑，它們各自的時間總量肯定相等，即可完工的總工期。

關鍵路徑是相對的，也可以是變化的。在採取一定的技術組織措施之後，關鍵路徑有可能變為非關鍵路徑，而非關鍵路徑也有可能變為關鍵路徑。

在項目管理中，編製網路計劃的基本思想就是在一個龐大的網路圖中找出關鍵路徑，並對各關鍵活動，優先安排資源，挖掘潛力，採取相應措施，盡量壓縮需要的時間。而對非關鍵路徑的各個活動，只要在不影響工程完工時間的條件下，抽出適當的人力、物力和財力等資源，用在關鍵路徑上，以達到縮短工程工期，合理利用資源等目的。在執行計劃過程中，可以明確工作重點，對各個關鍵活動加以有效控制和調度。

目標一：時間優化，即根據對計劃進度的要求，縮短項目工程的完工時間。

可供選擇的方案：

1． 採取先進技術的措施如引入新的生產機器等方式，縮短關鍵活動的作業時間；

2． 利用快速跟進法，找出關鍵路徑上的哪個活動可以并行；

3． 採取組織措施，充分利用非關鍵活動的總時差，利用加班、延長工作時間、倒班制和增加其它資源等方式合理調配技術力量及人、財、物等資源，縮短關鍵活動的作業時間。

目標二：時間－資源優化，在考慮工程進度的同時，考慮盡量合理利用現有資源，並縮短工期，具體要求和做法是：

1． 優先安排關鍵活動所需要的資源；

2． 利用非關鍵活動的總時差，錯開各活動的開始時間，拉平資源所需要的高峰，即人們常說的“削峰填谷”；

3． 在確實受到資源限制，或者在考慮綜合經濟效益的條件下，也可以適當地推遲工程時間。

目標三：時間－費用優化。這個目標包括兩個方面，一個是指在保證既定的工程完工時間的條件下，所需要的費用最少；或者是在限制費用的條件下，工程完工時間最短。

一般來講，工程費用可分為直接費用和間接費用兩大類，其中直接費用包括直接生產的工人工資及附加費，設備折舊、能源、工具及材料消耗等直接與完成活動有關的費用。為縮短活動的作業時間，需要採取一定的技術組織措施，相應地需要增加一部分直接費用，如為了趕工增加設備或者單位時間內增加能源消耗等。因此，在一定條件下和一定範圍內，活動的作業時間越短，直接費用越多。間接費用通常包括管理人員的工資、辦公費等，從成本會計上，我們把間接費用按照工程的施工時間進行直接分攤。在一定的生產規模內，活動的作業時間越短，分攤的間接費用也越少。因此，我們有以下時間-費用函數： Y = f1(t) + f2(t)

Y：總費用

f1(t)：直接費用

f2(t)：間接費用

該方程式表明，工程項目的不同完工時間所對應的活動總費用和工程項目所需要的總費用隨著時間的變化而變化。假設當 t = T’ 時，Y’ = Min(Y) 即工程總費用達到最低點，我們將T’點稱為最低成本日程(我們可以用一階導數為零,二階導數為正來求得T’點)。在制訂網路計劃時，無論是以降低費用為主要目標，還是盡量縮短工程完工時間為主要目標，都要計算最低成本日程，從而擬定出時間-費用的優化方案。

從上面的分析可以看出，CPM主要是一種基於單點時間估計、有嚴格次序的一種網路圖。它的出現為項目提供了重要的幫助，特別是為項目及其主要活動提供了圖形化的顯示，這些量化信息為識別潛在的項目延遲風險提供極其重要的依據。但是，我們也應用看到其不足之處：首先，現實生活中的項目網路往往包括上千項活動，在制定網路圖時，極其容易遺漏；其次，各個工資之間的優先關係未必十分明確，難以做圖；最後是各個活動時間經常需要利用概率分佈來估計時間點，有可能發生的偏差；最後，確定關鍵路徑目標其實質上為了確保項目按照這一特定的順序嚴格執行，從而不至於使整個項目停頓、拖延，如果管理團隊對確實無法確定的工作，就應該在項目運作的計劃中進行充分的分析和重新安排，此是網路計劃顯得無能為力。因此在項目中，CPM也需要其它工具和方法同時輔助使用。

計劃評審方法（program evaluation and review technique, PERT）和關鍵路線法Critical Path Method,CPM)是網路分析的重要組成部分，它廣泛地用於系統分析和項目管理，計劃評審與關鍵路線方法是在20世紀50年代提出並發展起來的。1956年，美國杜邦公司為了協調企業不同業務部門的系統規劃，提出了關鍵路線法。1958年，美國海軍武裝部在研製“北極星”導彈計劃時，由於導彈的研製系統過於龐大、複雜，為找到一種有效的管理方法，設計了計劃評審方法。由於PERT與CPM既有著相同的目標應用，又有很多相同的術語，這兩種方法已合併為一種方法，在國外稱為PERT/CPM，在國內稱為統籌方法（scheduling method）。