BCH碼

它的生成多項式與最小碼距之間有密切的關係，人們可以根據所要求的糾錯能力t很容易構造出BCH碼，它們的解碼器也容易實現，是線性分組碼中應用最普遍的一類碼。

本原循環碼是一類重要的碼。漢明碼、BCH碼和某些大數邏輯可解碼都是本原碼。本原碼的特點是:

1、碼長為2^m - 1，m為整數。

2、它的生成多項式由若干m階或以m的因子為最高階的多項式相乘構成。

要判斷循環碼是否存在，只需判斷階生成多項式是否能由的因式構成。

代數理論告訴我們，每個m階既約多項式一定能除盡。例如，m=5，共有6個5階既約多項式：

這6個多項式都能除盡。且必定是的因式。

若循環碼的生成多項式具有如下形式：

，這裡t為糾錯個數，為最小多項式，LCM表示取最小公倍式，則由此生成的循環碼稱之為BCH碼。該碼是以三個發現者博斯（Bose）、查德胡里（Chaudhuri）和霍昆格姆（Hocquenghem）名字的開頭字母命名的。其最小碼距dmin≥2t＋1，能糾t個錯誤。BCH的碼長為n＝或的因子。碼長為n＝的BCH碼稱為本原BCH碼。碼長為因子的BCH碼稱為非本原BCH碼。對於糾t個錯誤的本原BCH碼，其生成多項式為。糾正單個錯誤的本原BCH碼就是循環漢明碼。

下面介紹幾種常見的BCH碼。

1、戈雷碼（Golay）

（23，12）碼是一個特殊的非本原BCH碼，稱為戈雷碼，它的最小碼距7，能糾正3個錯誤，其生成多項式為。它也是目前為止發現的唯一能糾正多個錯誤的完備碼。

2、擴展形式

實際應用中，為了得到偶數碼長，並增加檢錯能力，可以在BCH碼的生成多項式中乘D+1，從而得到（n+1，k+1）擴展BCH碼。擴展BCH碼相當於將原有BCH碼再加上一位的偶校驗，它不再有循環性。

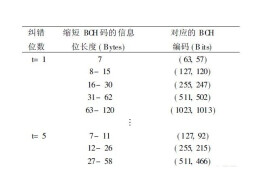
3、縮短形式

幾乎所以的循環碼都存在它另一種縮短形式。實際應用中，可能需要不同的碼長不是或它的因子，我們可以從碼中挑出前s位為0的碼組構成新的碼，這種碼的監督位數不變，因此糾錯能力保持不變，但是沒有了循環性。

BCH碼的解碼方法可以有時域解碼和頻域解碼兩類。頻移解碼是把每個碼組看成一個數字信號，把接受到的信號進行離散傅氏變換(DFT)，然後利用數字信號處理技術在“頻域”內解碼，最後進行傅氏反變換得到解碼后的碼組。時域解碼則是在時域直接利用碼的代數結構進行解碼。BCH的時域解碼方法有很多，而且糾多個錯誤的BCH碼解碼演演算法十分複雜。常見的時域BCH解碼方法有彼得森解碼、迭代解碼等。BCH的彼得森解碼基本過程為：1、用的各因式作為除式，對接收到的碼多項式求余，得到t個余式，稱為“部分校驗式”。2、用t個部分校驗式構造一個特定的解碼多項式，它以錯誤位置數為根。3、求解碼多項式的根，得到錯誤位置。4、糾正錯誤。具體內容可參閱參考資料[2]的第357－359頁。

事實上，BCH碼是一種特殊的循環碼，因此它的編碼器不但可以象其它循環碼那樣用除法器來實現，而且原則上所有適合循環碼解碼的方法也可以用於BCH碼的解碼。

RS碼是Reed-Solomon碼（理德－所羅門碼）的簡稱，它是一類非二進位BCH碼，在RS碼中，輸入信號分成k·m比特一組，每組包括k個符號，每個符號由m個比特組成，而不是前面所述的二進位碼由一個比特組成。

一個糾t個符號錯誤的RS碼有如下參數：

碼長：符號，或比特

信息段：符號，或比特

監督段：符號或比特

最小碼距：符號或比特

RS碼非常適合於糾正突發錯誤。它可以糾正的錯誤圖樣有：

總長度為比特的單個突發

總長度為比特的兩個突發

。。。

總長度為比特的i個突發。

對於一個長度為符號的RS碼，每個符號都可以看成是有限域GF（）中的一個元素。最小碼距為d符號的RS碼的生成多項式具有如下形式：

這裡，是GF（）中的一個元素。例如，構造一個能糾3個錯誤符號，碼長為15，m＝4的RS碼，由RS碼的參數可知，該碼的碼距為7，監督段為6個符號。因此該碼為（15，9）RS碼。生成的多項式為：

所以從二進位角度看，這是一個（60，36）碼。

分組糾錯碼的模擬

前面介紹了各種分組糾錯碼的原理及相關內容。不難看出，無論是何種編碼，其編碼、解碼都是相對複雜的，除了複雜的數學模型外，其實際電路也非常繁雜。為方便用戶對分組糾錯碼的模擬和性能研究，SystemView在通信庫中提供了專門的分組糾錯編碼（BlkCode）、解碼（BlkDecode）的圖符庫。用戶只需要在相應的參數輸入欄內填入相應參數即可獲得BCH碼、RS碼、和Golay碼（註：因為戈雷碼為（23，12）碼，所以編碼其參數是確定的，用戶無需輸入參數）。圖12.18所示為分組糾錯碼的參數輸入窗口。在“CodeLength”內

可以輸入碼的長度n，在“InformationBits”內可以輸入信息碼的長度k，在“Correct”內可以輸入能糾錯的位數t。單擊單選框“SelectBlockCode”內的選項可以選擇BCH碼、RS碼和Golay碼。

圖12.19所示是利用分組糾錯碼圖符建立的一個Golay碼編碼、解碼以及信號在高斯雜訊通道上傳輸誤碼率測試的模擬原理圖。同樣也可以將編解碼器設置為其它BCH碼類型。在使用RS碼時，因為RS碼為非二進位碼，因此在進入編碼之前，應對二進位數據信號進行比特符號轉換。圖12.20是RS碼的編解碼模擬實驗原理圖。實驗中使用的是（15，11）RS碼，中間使用了比特符號和符號比特轉換器，轉換參數為每符號4比特。信號源使用4Hz的PN碼。通道中的雜訊用高斯雜訊信號源來模擬，並使用了一個放大器作為信噪比控制器。

分組碼就其構成方式可分為線性分組碼與非線性分組碼。

線性分組碼是指[n,M]分組碼中的M個碼字之間具有一定的線性約束關係，即這些碼字總體構成了n維線性空間的一個κ維子空間。稱此κ維子空間為(n，κ)線性分組碼，n為碼長，κ為信息位。此處M=2。

非線性分組碼[n，M]是指M個碼字之間不存在線性約束關係的分組碼。d為M個碼字之間的最小距離。非線性分組碼常記為[n，M，d]。非線性分組碼的優點是：對於給定的最小距離d,可以獲得最大可能的碼字數目。非線性分組碼的編碼和解碼因碼類不同而異。雖然預料非線性分組碼會比線性分組碼具有更好的特性，但在理論上和實用上尚缺乏深入研究（見非線性碼）。

用Vn表示GF(2)域的n維線性空間，Vκ是Vn的κ維子空間，表示一個(n，κ)線性分組碼。Ei=（vi1，vi2…,vin）是代表Vκ的一組基底(i=1，2，…，κ)。以這組基底構成的矩陣

稱為該(n,κ)線性碼的生成矩陣。對於給定的消息組m=(m1，m2，…，mκ)，按生成矩陣G，m被編為mG=m1E1+m2E2+…+mκEκ

這就是線性分組碼的編碼規則。若

之秩為n-κ並且滿足GH=0，僅當=(v1,v2,…，vn)∈n滿足H=0時，才為κ中的碼字。稱H為(n，κ)線性分組碼κ的均等校驗矩陣，稱H為矢量的伴隨式。假設v是發送的碼矢量，在接收端獲得一個失真的矢量r=v+E,式中E=(e1，e2，…，en)稱為錯誤型。由此rH=(v+e)H=eH

線性碼的解碼原則便以此為基礎。

這是最早提出的一類線性分組碼，已廣泛應用於計算機和通信設備。它是由R.W.漢明於1950年提出的。若碼的均等校驗矩陣H由2-1個、按任一次序排列且彼此相異的二進位r維列矢量構成。這樣得到的線性分組碼稱為漢明碼，其分組長為n=2-1，信息位為κ=n-r=2-1-r，即為(2-1，2-1-r)碼。例如，以矩陣

為均等校驗矩陣的線性分組碼便為(7，4)漢明碼。漢明碼的解碼十分簡單。例如, 假定=(1001100)為發送的碼字，其第3位有錯，即接收矢量為r=(1011100)。於是

恰為矩陣H的第 3 列，因而判定原來發送的碼字為=(1001100)。這種解碼方式是一般性的。如果接收矢量r在第i位有錯，則其伴隨式Hr剛好為矩陣H的第i列。漢明碼是可以糾正單個錯誤的線性分組碼。

具有某種循環特性的線性分組碼，如果(n，κ)線性分組碼Vκ具有如下的性質：對於每一個=(ɑ0,ɑ1，…，)∈Vn，只要∈Vκ,其循環移位()亦屬於Vκ,則稱Vκ為循環碼。循環碼的優點在於其編碼和解碼手續比一般線性碼簡單，因而易於在設備上實現。使Vn中的每一個矢量=(ɑ0，ɑ1，…，),對應於域GF(2)上的多項式ɑ(x)=ɑ0+ɑ1x+…+x。於是Vn中的全體n維矢量便與上述多項式之間建立了一一對應的關係。基於這種對應，使Vn中除了線性運算而外，還建立了矢量之間的乘法運算。A=(ɑ0,ɑ1,…,)與B=(b0,b1,…,)的乘積ab可視為ɑ(x)b(x)[mod(x-1)]所對應的矢量。因此，一個(n,κ)循環碼的生成矩陣及均等校驗矩陣可分別由生成多項式及均等校驗多項式h(x)所代替，從而簡化了編碼及解碼運算。

這是一種重要的線性分組碼，它不僅包括常見的諸如本原BCH碼等大量的循環碼類，還包括相當多的非循環線性分組碼類，並且后一種碼具有良好的漸近特性。戈帕碼的理論實質在於將每一個碼矢量與一個有理分式相對應。q是某一個素數冪，g(z)是域GF(q)上的任意多項式，L表示域GF(q)中所有不為g(z)之根的元素所成之集合，|L|代表L中元素的數目。於是存在一個以GF(q)為符號域，以GF(q)為位置域的線性分組碼。碼長為|L|，它的各碼元用L中的元素來標誌。這種碼可定義為滿足條件

的一切GF(q)上的全體|L|維矢量的集合，式中 這種碼稱為戈帕碼，稱g(z)為戈帕多項式。

例如，q=2,m=2，g(z)=z+α,α是域GF(z)上的本原元素　α+α+1=0　α3=1

則

於是

可驗證,(1，1，1)即為這一戈帕碼的碼字。戈帕碼也有類似於BCH碼的解碼方法。

自50年代分組碼的理論獲得發展以來，分組碼在數字通信系統和數據存儲系統中已被廣泛應用。由於大規模和超大規模集成電路的迅速發展，人們開始從易於實現的循環碼理論研究中解脫出來，更重視研究性能良好的非循環線性分組碼和非線性分組碼。人們在分組碼研究中又引進了頻譜方法，這一研究方向受到了較多的注意。

其他碼制

---

里德-索洛蒙碼

這是一種特殊的非二進位BCH碼。對於任意選取的正整數s,可構造一個相應的碼長為n=q-1的q進位BCH碼，其中碼元符號取自有限域GF(q)，其中q為某一素數的冪。當s=1,q>2時所建立的碼長為n=q-1的q進位BCH碼便稱為里德-索洛蒙碼，簡稱為RS碼。當q=2(m>1),碼元符號取自域GF(2)的二進位RS碼可用來糾正成區間出現的突發錯誤。這種碼在短波通道中特別有用。

相關詞條

---

礦石	導電性	磁性
放射性	光學性質	物理特性