指數積分
指數積分
對任意實數,指數積分有下定義:
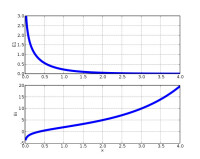
E1函數(頂)和Ei函數(底)。
如果自變數是複數的情形,這個定義就變得模稜兩可了。為了避免歧義,我們使用以下的記法:
如果,則
其中,
收斂級數
其中γ是歐拉常數。
漸進(發散)級數
自變數的值較大時,用以上的收斂級數來計算指數積分是困難的。在這種情況下,我們可以使用發散(或漸近)級數:
指數和對數的表現
E1在自變數較大時的表現類似指數函數,自變數較小時類似對數函
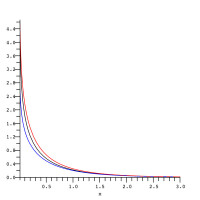
指數積分
這個不等式的左端在圖中用紅色曲線來表示,中間的黑色曲線是E1(x),不等式的右端用藍色曲線來表示。
與其它函數的關係
指數積分與對數積分li(x)的關係:
另外一個有密切關係的函數,具有不同的積分限:
可以延伸到負數:
我們可以把兩個函數都用整函數來表示:
此函數的性質:
指數積分還可以推廣為:
導數
函數En與E1的導數有以下簡單的關係:
然而,這裡假設了n是整數;複數n的推廣還沒有在文獻中報導,雖然這種推廣是有可能的。
復變數的指數積分
從定義中可以看出,指數積分與三角積分之間的關係:
圖中的黑色和紅色曲線分別描述了的實數和虛數部分。
