共找到9條詞條名為彈性力學的結果 展開
彈性力學
固體力學的重要分支

彈性力學
彈性力學的發展大體分為四個時期。

彈性力學
第二個時期是理論基礎的建立時期。這個時期的主要成就是,從1822~1828年間,在A.-L·柯西發表的一系列論文中明確地提出了應變、應變分量、應力和應力分量概念,建立了彈性力學的幾何方程、平衡(運動)微分方程,各向同性和各向異性材料的廣義胡克定律,從而為彈性力學奠定了理論基礎。
第三個時期是線性各向同性彈性力學大發展時期。這個時期的主要特點是彈性力學被廣泛應用於工程問題,同時在理論方面建立了許多重要的定理和原理,並提出了許多有效的計算方法。這個時期從A·J·C·B·de聖維南於1855~1856年間發表關於柱體的扭轉和彎曲的論文後開始,開闢了一條用半物理半數學的方法解彈性力學基本方程的途徑。接著G·B·艾里解決了平面應力問題,H·R·赫茲解決了接觸問題,G·基爾施解決了孔邊應力集中問題,等等。這些成就的取得,使彈性力學得到工程界的重視。在這個時期中,彈性力學的一般理論也有了很大的發展。在彈性力學基本方程建立后不久,建立了彈性力學的虛功原理和最小勢能原理。1872年E.貝蒂建立了互換定理。1879年A·卡斯蒂利亞諾建立了余能原理。由於這些能量原理的建立,使基於這些原理的近似計算(如瑞利-里茲法和伽遼金法)也得到了發展。
從20世紀20年代起,彈性力學進入第四個時期,各向異性和非均勻體的彈性力學、非線性彈性力學、熱彈性力學等都有了重大發展。另外,還出現了許多邊緣分支,如研究固體與氣體(或液體)共同作用的氣動彈性力學以及粘彈性力學等。這些領域的發展,促進了有關工程技術的發展。

彈性力學
求解一個彈性力學問題,就是設法確定彈性體中各點的位移、應變和應力共15個函數。從理論上講,只有15個函數全部確定后,問題才算解決。但在各種實際問題中,起主要作用的常常只是其中的幾個函數,有時甚至只是物體的某些部位的某幾個函數。所以常常用實驗和數學相結合的方法,就可求解。數學彈性力學的典型問題主要有一般性理論、柱體扭轉和彎曲、平面問題、變截面軸扭轉,迴轉體軸對稱變形等方面。
在近代,經典的彈性理論得到了新的發展。例如,把切應力的成對性發展為極性物質彈性力學;把協調方程(保證物體變形后連續,各應變分量必須滿足的關係)發展為非協調彈性力學;推廣胡克定律,除機械運動本身外,還考慮其他運動形式和各種材科的物理方程稱為本構方程。對於彈性體的某一點的本構方程,除考慮該點本身外還要考慮彈性體其他點對該點的影響,發展為非局部彈性力學等。
1.假定物體是連續的,就是假定整個物體的體積都被組成這個物體的介質所填滿,不留下任何空隙。
2.假定物體是完全彈性的,就是假定物體完全服從胡克定律——應變與引起該應變的那個應力分量成比例。
3.假定物體是均勻的,就是整個物體是由同一材料組成的。
4.假定物體是各向同性的,就是物體內一點的彈性在所有各個方向都相同。
5.假定位移和形變是微小的。
主要分支
靜力學、動力學、流體力學、分析力學、運動學、固體力學、材料力學、複合材料力學、流變學、結構力學、彈性力學、塑性力學、爆炸力學、磁流體力學、空氣動力學、理性力學、物理力學、天體力學、生物力學、計算力學
物理分支
物理學概覽、力學、熱學、光學、聲學、電磁學、核物理學、固體物理學
在各向同性線性彈性力學中,為了求得應力、應變和位移,先對構成物體的材料以及物體的變形作了五條基本假設,即:連續性假設、均勻性假設、各向同性假設、完全彈性假設和小變形假設,然後分別從問題的靜力學、幾何學和物理學方面出發,導得彈性力學的基本方程和邊界條件的表達式。
直角坐標系下的彈性力學的基本方程為平衡微分方程:
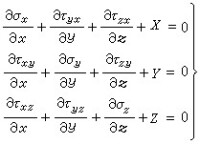
彈性力學
幾何方程:
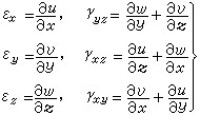
彈性力學
物理方程:
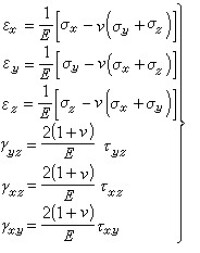
彈性力學
(1)式中的σx、σy、σz、τyz=τzy、τxz=τzx、τxy=τyx為應力分量,X、Y、Z為單位體積的體力在三個坐標方向的分量;(2)式中的u、v、w為位移矢量的三個分量(簡稱位移分量),εx、εy、εz、γyz、γxz、γxy為應變分量;(3)式中的E和v分別表示楊氏彈性模量和泊松比。
在物體的表面,如已知面力,則邊界條件表示為
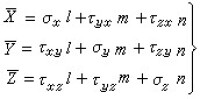
彈性力學
這裡的 塣、墏、墫表示作用在物體表面的單位面積上的面力矢量的三個分量,l、m、n表示物體表面外法線的三個方向餘弦。
如物體表面位移ū、堸、塐已知,則邊界條件表示為
u=ū,v=堸,w=塐 (5)
這樣就將彈性力學問題歸結為在給定的邊界條件下求解一組偏侮分方程的問題。
主要解法式(1)、(2)、(3)中有15個變數,15個方程,在給定了邊界條件后,從理論上講應能求解。但由(2)、(3)式可見,應變分量、應力分量和位移分量之間不是彼此獨立的,因此求解彈性力學問題通常有兩條途徑。其一是以位移作為基本變數,歸結為在給定的邊界條件下求解以位移表示的平衡微分方程,這個方程可以從(1)、(2)、(3)式中消去應變分量和應力分量而得到。其二是以應力作為基本變數,應力分量除了要滿足平衡微分方程和靜力邊界條件外,為保證物體變形的連續性,對應的應變分量還須滿足相容方程:

彈性力學
這組方程由幾何方程消去位移分量而得到。對於不少具體問題,上述方程還可以簡化。
在彈性力學中,為克服求解偏微分方程(或方程組)的困難,通常採用試湊法,即根據物體形狀的幾何特性和受載情況,去試湊位移分量或應力分量;由彈性力學解的唯一性定理,只要所試湊的量滿足全部方程和全部邊界條件,即為問題的精確解。
從數學觀點來看,彈性力學方程的定解問題可變為求泛函的極值問題。例如,對於用位移作為基本變數求解的問題,又可以歸結為求解變分方程:
δП1=0 (7)
П1是物體的總勢能,它是一切滿足位移邊界條件的位移的泛函。對於穩定平衡狀態,精確的位移將使總勢能П1取最小值的稱為最小勢能原理。又如對於用應力作為基本變數求解的問題,可歸結為求解變分方程:
δП2=0 (8)
П2為物體的總余能,它是一切滿足平衡微分方程和靜力邊界條件的應力分量的泛函。精確的應力分量將使總余能 П2取最小值的稱為最小余能原理。(7)式等價於用位移表示的平衡微分方程和靜力邊界條件,而(8)式則等價於用應

彈性力學
還有各種所謂的廣義變分原理,其中最一般的是廣義勢能原理和廣義余能原理,它們等價於彈性力學的全部基本方程和邊界條件。但和總勢能П1和總余能П2不同,廣義勢能和廣義余能作為應力分量、應變分量和位移分量的泛函,對於精確解,也只取非極值的駐值。
由於彈性力學的基本方程是在彈性力學的五條基本假設下通過嚴密的數學推導得出的,因此彈性力學又稱為數學彈性力學。而板殼力學則屬於應用彈性力學。因為,它除了引用這五條基本假設外,還對變形和應力的分佈作了一些附加假設。從這個意義上講,材料力學也可納入應用彈性力學。可見,雖然彈性力學和材料力學都研究桿狀構件,但前者所獲得的結果是比較精確的。
為了闡明一個彈件力學問題,需要說明物體的形狀和物體的各部分由什麼材料組成(直接給出物體各部分的廣義胡克定律當然更好);說明物體所承受的載荷,包括體積力fi、自由邊界上的載荷;說明此物體和其他物體的連接情況。例如,所考慮的對象是物體Q,它在邊界B1和B2同另兩個物體Q1和Q2相連接。如果Q1的剛度比Q大得多,則B1上各點的位移就基本上由Q1的位移決定。這樣,對Q來說,B1上各點的位移是由外界給定的,因而有位移邊界條件(2)。如果Q2的剛度比Q小得多,則Q2基本上不能限制B2上各點的位移。這樣,對Q來說,B2可看作是自由的,因而有載荷的邊界條件(9)。如果Q1或Q2的剛度同Q相差不多,要建立恰當的邊界條件就不那麼容易,須就具體情況作細緻的分析。
對彈性力學的平衡問題,說明上述三個方面便可以了。但對彈性力學的動力問題,還需說明物體的初始狀態,即
當t=t0時,
式中t0為初始時間,ut0和vt0分別為物體在初始時刻的位移和速度,它們應是給定的函數。
求解一個彈性力學問題,就是設法確定彈性體中各點的位移、應變和應力共15個函數。從理論上說,只有15個函數全部確定后,問題才算徹底解決。但在各種具體問題中,常常只關心其中的某幾個函數,有時甚至只關心物體的某些部位的某幾個函數。所以在實用上,常常不需要確定全部函數。求解時,可用實驗方法、數學方法,也可用實驗和數學相結合的方法。
實驗方法是用機械的、電的、光的以及其他手段在實物上或在模型上測量所需的量。許多複雜而難於計算的問題都是用實驗方法求解的(見實驗應力分析)。
數學方法就是根據幾何方程(1)、應力-應變關係(3a)或(3b)、運動(或平衡)微分方程(5)、邊界條件(2)和(9)以及動力問題中的初始條件(10),解出ui、、等15個函數。學方法的優點是提供的數據比較全面,但當前只適用於不太複雜的問題。這方面的研究構成了以數學方法為主要研究手段的數學彈性力學。
對於一些實用上重要的彈性力學問題,常需要同時用實驗和數學兩種方法求解,以保證結論的可靠性。
彈性力學中常用的數學方法可分分成兩類:
①精確解法 包括分離變數法和彈性力學的複變函數方法。彈性力學中的許多精確解是用分離變數法求得的。其步驟大致如下:根據物體的形狀,選擇一種合適的曲線坐標系,並寫出相應於該坐標系的彈性力學微分方程和邊界條件,如果微分方程中的變數能夠分離,通常便可求得問題的解。能用分離變數法求得精確解的問題有:無限和半無限體的問題,球體和球殼的問題,橢球腔的問題,圓柱和圓盤的問題等。
對於能化為平面調和函數或平面雙調和函數的問題,複變函數方法是一個有效的求解工具《柱體的扭轉和彎曲問題、平面應變和平面應力問題以及薄板彎曲問題中的許多重要精確解都是用複變函數法求得的。
②近似解法 為求解一些複雜的問題,在彈性力學中還發展了許多近似解法,能量法就是其中用得最多的一類方法,它把彈性力學問題化為數學中的變分問題(泛函的極值和駐值問題),然後再用瑞利-里茲法求近似解。能量法的內容很豐富,適應性很強。工程界當前廣泛使用的有限元法是能量法的一種新發展。差分法也是一種常用的近似解法,其要點是用差商近似地代替微商,從而把原有的微分方程近似地化為代數方程。此外,邊界積分方程、邊界元法和加權殘數法對解決某些問題也是有效的手段。
數學彈性力學的典型問題 有以下幾類:
①一般性理論 它探討解的共性和一般性的求解方法。一般性理論中,最核心的部分是能量原理(定理),包括虛功原理(虛位移原理、虛應力原理)、功的互等定理、最小勢能原理、最小余能原理、赫林格-瑞斯納二類變數廣義變分原理和胡海昌-鷲津久一郎三類變數廣義變分原理等。解的存在性、唯一性、解析性、平均值定理以及近似解的收斂性等,也都和能量原理有密切聯繫。這些一般性理論,是建立各種近似解法和建立工程結構實用理論的依據。
一般性理論的另一重要方面是未知函數的歸併理論,其主要內容是將彈性力學問題歸為求解少數幾個函數,這些函數常稱為應力函數和位移函數。
②柱體扭轉和彎曲 一個側面不受外力的細長柱體,在兩端面上的外力作用下會產生扭轉和彎曲。根據聖維南原理,柱體中間部分的應力狀態只與作用在端面上載荷的合力和合力矩有關,而與載荷的具體分佈無關。因此,柱體中間部分的應力有以下的表達式:
這裡的x、y軸為橫截面的兩個主軸;z軸平行於柱體的母線;為應力分量,A為橫截面的面積;Ix和Iy為橫截面對x軸和y軸的慣性矩(見截面的幾何性質);N、Mx和My分別為作用在截面上的軸向合力、對x軸和y軸的彎矩。彎矩Mx、My是坐標z的線性函數,可用材料力學的方法求得。式(11)給出的與材料力學的解相同,但給出的剪應力比材料力學的結果精確。決定的問題最後可歸為求解一個平面調和函數的邊值問題。
③平面問題 平面問題是彈性力學中發展得比較成熟,應用得比較廣的一類問題。平面問題可分為平面應力問題和平面應變問題。兩者的應用對象不同,但都可歸為相同的數學問題——平面雙調和函數的邊值問題.
圖1 平面應力問題
平面應力問題適用於薄板。若在薄板的兩個表面上無外力,而在側面上有沿厚度均勻分佈的載荷(圖1),則薄板中的位移和應力有如下特點:
且以及x、y方向的位移u、v都與坐標z無關。對於各向同性材料,上述五個不等於零的量可以用一個應力函數φ(x,y)(艾里應力函數)表示為:
而應力函數φ是一個平面雙調和函數,即
平面應變問題適用於長柱體的中間部分。若柱體的兩端面固定不動,而作用在側面上的載荷和坐標z無關,且合力及合力矩等於零(圖2),則柱體中間部分的應力和位移有如下特點:
縱向位移ω=0,且、u、v與坐標z無關。對於各向同性的材料,上述五個不等於零的量也可用一個雙調和函數φ表示為公式(13),不過須將其中的E和v分別代以
圖2 平面應變問題
④變截面軸扭轉變截面軸受扭時,在截面的過渡區(圖3)常有應力集中現象。分析這類問題以取圓柱坐標系(r,θ,z)為方便。在圓柱坐標系中的位移分量和應力分量分別記為u、v、w和
這類問題的力學特點是: u=w=0和
v、和與坐標z無關。上述不等於零的兩個剪應力和可用一個應力函數(r,z)表示為:
而滿足下列偏微分方程:
這類問題最後歸為方程(15)的邊值問題。
圖3 變截面軸的過渡區示意圖
⑤迴轉體的軸對稱變形各向同性的迴轉體在軸對稱載荷作用下,必然產生軸對稱的變形。在圓柱坐標系(r,θ,z)中,軸對稱變形的特點是:v=0,=,且u、w、、、和與坐標θ無關。上述不等於零的六個量,可以用一個位移函數(x,y)表示為:
其中△是軸對稱的拉昔拉斯算符,即
而是軸對稱的雙調和函數,即
⑥工程結構元件的實用理論 從廣義上說,各種工程結構元件的實用理論(如桿、板、殼的實用理論)都是彈性力學的特殊分支,而且是最有實用價值的分支。這些實用理論分別依據結構元件形狀及其受力的特點,對位移分佈作一些合理的簡化假設,對廣義胡克定律也作相應的簡化。這樣,就能使數學方程既得到充分簡化又保留了主要的力學特性。從彈性力學看,這些結構元件的實用理論都是近似理論,其近似性大多表現為按照這些理論計算得到的應力和應變不能嚴格滿足胡克定律。