牛頓迭代法
17世紀牛頓提出的方法
牛頓迭代法(Newton's method)又稱為牛頓-拉夫遜(拉弗森)方法(Newton-Raphson method),它是牛頓在17世紀提出的一種在實數域和複數域上近似求解方程的方法。
牛頓迭代法
牛頓迭代法
牛頓迭代法
多數方程不存在求根公式,因此求精確根非常困難,甚至不可能,從而尋找方程的近似根就顯得特別重要。方法使用函數 的泰勒級數的前面幾項來尋找方程 的根。牛頓迭代法是求方程根的重要方法之一,其最大優點是在方程 的單根附近具有平方收斂,而且該法還可以用來求方程的重根、復根,此時線性收斂,但是可通過一些方法變成超線性收斂。另外該方法廣泛用於計算機編程中。
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
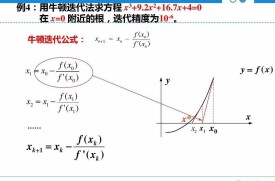
設 是 的根,選取 作為 的初始近似值,過點 做曲線 的切線, ,則 與 軸交點的橫坐標,稱 為 的一次近似值。過點 做曲線 的切線,並求該切線與x軸交點的橫坐標,稱 為r的二次近似值。重複以上過程,得 的近似值序列,其中,稱為 的 次近似值,上式稱為 牛頓迭代公式。
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
用牛頓迭代法解非線性方程,是把非線性方程 線性化的一種近似方法。把 在點 的某鄰域內展開成泰勒級數,取其線性部分(即泰勒展開的前兩項),並令其等於0,即,以此作為非線性方程 的近似方程,若,則其解為,這樣,得到牛頓迭代法的一個迭代關係式: 。
已經證明,如果是連續的,並且待求的零點是孤立的,那麼在零點周圍存在一個區域,只要初始值位於這個鄰近區域內,那麼牛頓法必定收斂。並且,如果不為0, 那麼牛頓法將具有平方收斂的性能. 粗略的說,這意味著每迭代一次,牛頓法結果的有效數字將增加一倍。
迭代法也稱輾轉法,是一種不斷用變數的舊值遞推新值的過程,跟迭代法相對應的是直接法(或者稱為一次解法),即一次性解決問題。迭代演演算法是用計算機解決問題的一種基本方法。它利用計算機運算速度快、適合做重複性操作的特點,讓計算機對一組指令(或一定步驟)重複執行,在每次執行這組指令(或這些步驟)時,都從變數的原值推出它的一個新值。
利用迭代演演算法解決問題,需要做好以下三個方面的工作:
一、確定迭代變數
在可以用迭代演演算法解決的問題中,至少存在一個可直接或間接地不斷由舊值遞推出新值的變數,這個變數就是迭代變數。
二、建立迭代關係式
所謂迭代關係式,指如何從變數的前一個值推出其下一個值的公式(或關係)。迭代關係式的建立是解決迭代問題的關鍵,通常可以使用遞推或倒推的方法來完成。
三、對迭代過程進行控制
在什麼時候結束迭代過程?這是編寫迭代程序必須考慮的問題。不能讓迭代過程無休止地執行下去。迭代過程的控制通常可分為兩種情況:一種是所需的迭代次數是個確定的值,可以計算出來;另一種是所需的迭代次數無法確定。對於前一種情況,可以構建一個固定次數的循環來實現對迭代過程的控制;對於后一種情況,需要進一步分析得出可用來結束迭代過程的條件。
最經典的迭代演演算法是歐幾里德演演算法,用於計算兩個整數a,b的最大公約數。其計算原理依賴於下面的定理:
定理:gcd(a,b) = gcd(b,a mod b)
證明:a可以表示成a = kb + r,則r = a mod b。假設d是a,b的一個公約數,則有 a%d==0,b%d==0,而r = a - kb,因此r%d==0 ,因此d是(b,a mod b)的公約數
同理,假設d 是(b,a mod b)的公約數,則 b%d==0,r%d==0 ,但是a = kb +r ,因此d也是(a,b)的公約數。
因此(a,b)和(b,a mod b)的公約數是一樣的,其最大公約數也必然相等,得證。
從上面的程序我們可以看到a,b是迭代變數,迭代關係是temp = a % b;根據迭代關係我們可以由舊值推出新值,然後循環執a = b; b = temp;直到迭代過程結束(餘數為0)。在這裡a好比那個膽小鬼,總是從b手中接過位置,而b則是那個努力向前沖的先鋒。
還有一個很典型的例子是斐波那契(Fibonacci)數列。斐波那契數列為:0、1、1、2、3、5、8、13、21、…,即 fib⑴=0; fib⑵=1;fib(n)=fib(n-1)+fib(n-2) (當n>2時)。
在n>2時,fib(n)總可以由fib(n-1)和fib(n-2)得到,由舊值遞推出新值,這是一個典型的迭代關係,所以我們可以考慮迭代演演算法。
可以得到一元3次方程3個解的程序(原創,超優化):
function y=f(x)
y=f(x);%函數f(x)的表達式
end
function z=h(x)
z=h(x);%函數h(x)的表達式
end
x=X;%迭代初值
i=0;%迭代次數計算
while i<= 100%迭代次數
x0=X-f(X)/h(X);%牛頓迭代格式
if abs(x0-X)>0.01;%收斂判斷
X=x0;
else break
end
i=i+1;
end
fprintf('\n%s%.4f\t%s%d','X=',X,'i=',i) %輸出結果
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
牛頓迭代法
program newton
implicit none
real::a
real::b
real::fb
real::counter
integer::n
!real,parameter::zero=0.00001
real::fx,fx1
real::df
write(*,*)"enter a number:"
read(*,*)a
do counter=1,a-1
fx=sin(counter)
fx1=sin(counter+1)
if (fx*fx1<0) then
df=cos(counter)
fx=sin(counter)
write(*,*)"初始值取:"
write(*,*)counter
do n=1,25,1
b=counter-fx/df
fb=sin(b)
end do
write(*,*)"數值解:"
write(*,*)b
end if
end do
stop
end program

牛頓迭代法