三重積
三重積
三重積,又稱混合積,是三個向量相乘的結果。向量空間中,有兩種方法將三個向量相乘,得到三重積,分別稱作標量三重積和向量三重積。設 a ,b ,c 是空間中三個向量,則(a×b)·c 稱為三個向量 a ,b ,c 的混合積,記作[a b c] 或(a,b,c)或(abc)。
標量三重積是三個向量中的一個和另兩個向量的叉積相乘得到點積,其結果是個贗標量。
設為a,b,c為三個向量,則標量三重積的定義為。
設則有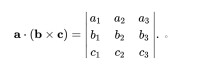
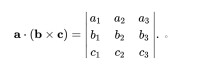
三重積
證明
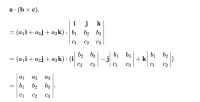
三重積
利用行列式的特性,可知順序置換向量的位置不影響標量三重積的值:
.
任意對換兩個向量的位置,標量三重積與原來相差一個負號:
若任意兩個向量相等,則標量三重積等於零:
有時候,標量三重積會以括弧表示:
幾何上,由三個向量定義的平行六面體,其體積等於三個標量標量三重積的絕對值:
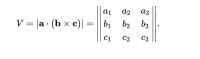
三重積
向量三重積是三個向量中的一個和另兩個向量的叉積相乘得到的叉積,其結果是個向量。
對於三個向量 a,b,c,向量三重積的定義為
。
值得注意的是,一般來說,
。
以下恆等式,稱作三重積展開或拉格朗日公式,對於任意向量a,b,c均成立:
.
英文中有對於第一式有助記口訣 (,後面的計程車),但是不容易記住第一式跟第二式的變化,很容易搞混。觀察兩個公式,可得到以下三點:
兩個分項都帶有三個向量;
三重積一定是先做叉積的兩向量之線性組合;
中間的向量所帶的係數一定為正(此處為向量b)。
證明
我們可以由叉積的定義計算的x分量:
類推至y和z分量,可得:
所以
。
利用上述恆等式,可得以下結果:
(雅可比恆等式)
在向量分析中,有以下與梯度相關的一條恆等式:
三重積