總體標準差
反映個體間差異程度的指標
總體標準差是總體各單位標誌值與其算術平均數之間的平均離差,用σ表示。總體方差是一組資料中各數值與其算術平均數離差平方和的平均數。總體標準差則是總體方差的平方根。
標準差是最常用和最重要的變異性測量。標準差以分佈的平均數作為參照點,用考慮每個數據和平均數之間的距離來測量變異性。它由數據是否接近或遠離平均數來決定。也就是說,它考慮數據是聚集還是離散的?簡單來說,標準差與數據到平均數的平均距離近似。
方差被定義為平方差的平均數。這個平均數為總和除以N,因此,總體方差的公式為:
方差=SS/N
標準差是方差的平方根,因此,總體標準差的公式為:
標準差=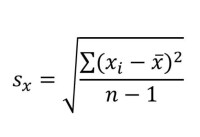
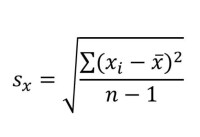
標準差
與平均數(μ)一樣,方差和標準差是總體的參數,將用希臘字母表示。我們用σ表示總體標準差。為了強調標準差和方差之間的關係,我們用σ表示總體方差。所以:
總體標準差
總體方差

總體標準差
總體參數中除了均值和比例的估計之外,還經常要對差異的情況作出估計,例如:一架飛機的電纜如果發生斷裂,飛機就會失去控制,因而嚴格控制其質量非常必要。但只知道電纜的平均強度是否達到標準是不夠的,因為如果電纜差異太大,電纜強度太強,都容易發生斷裂,後果不堪設想。所以對於電纜強度質量不僅應知道均值,而且還應知道方差,即需要要對電纜的方差進行估計。
對方差進行估計要用到Excel中的卡方分佈反函數CHIINV。若已知總體方差σ(總體方差未知時用樣本方差S代替總體方差)和樣本數,對於給定的顯著性水平σ,利用CHINV函數可以求出臨界值X和X1(N-1)
則總體方差σd的置信度為1−σ的置信區間為
其中,分別是自由度為n−1的X分佈的σ/2和1-σ/2的水平的分位數。
