電子衍射實驗

現代晶體生長過程中，用電子衍射方法進行監控，也十分普遍。1927年Davsso和Germer首次實驗驗證了De Broglie關於微觀粒子具有波粒二象性的理論假說，奠定了現代量子物理學的實驗基礎。本實驗主要用於多晶體的電子衍射現象，測量運動電子的波長；驗證德布羅意關係。

驗證電子具有波動性的假設；

了解電子衍射和電子衍射實驗對物理學發展的意義；

了解電子衍射在研究晶體結構中的應用；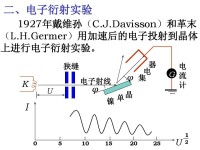

電子衍射，真空機組，複合真空計，數碼相機，微機

電子的波粒二象性

波在傳播過程中遇到障礙物時會繞過障礙物繼續傳播，在經典物理學中稱為波的衍射，光在傳播過程表現出波的衍射性，光還表現出干涉和偏振現象，表明光有波動性；光電效應揭示光與物質相互作用時表現出粒子性，其能量有一個不能連續分割的最小單元，即普朗克1900年首先作為一個基本假設提出來的普朗克關係

E為光子的能量，v為光的頻率，h為普朗克常數，光具有波粒二象性。電子在與電磁場相互作用時表現為粒子性，在另一些相互作用過程中是否會表現出波動性？德布羅意從光的波粒二象性得到啟發，在1923－1924年間提出電子具有波粒二象性的假設，

E為電子的能量，為電子的動量，為平面波的圓頻率，為平面波的波矢量，為約化普朗克常數；波矢量的大小與波長λ的關係為，稱為德布羅意關係。電子具有波粒二象性的假設，拉開了量子力學革命的序幕。

電子具有波動性假設的實驗驗證是電子的晶體衍射實驗。電子被電場加速后，電子的動能等於電子的電荷乘加速電壓，即考慮到高速運動的相對論效應，電子的動量由德布羅意關係得真空中的光速，電子的靜止質量，普朗克常數，當電子所受的加速電壓為V伏特，則電子的動能，電子的德布羅意波長，（1）

加速電壓為100伏特，電子的德布羅意波長為。要觀測到電子波通過光柵的衍射花樣，光柵的光柵常數要做到的數量級，這是不可能的。晶體中的原子規則排列起來構成晶格，晶格間距在的數量級，要觀測電子波的衍射，可用晶體的晶格作為光柵。1927年Davisson–Germer用單晶體做實驗，湯姆遜用多晶體做實驗，均發現了電子在晶體上的衍射，實驗驗證了電子具有波動性的假設。

普朗克因為發現了能量子獲得1918年諾貝爾物理學獎；德布羅意提出電子具有波粒二象性的假設。導致薛定諤波動方程的建立，而獲得1929年諾貝爾物理學獎；戴維孫和湯姆遜因發現了電子在晶體上的衍射獲得1937年諾貝爾物理學獎。

由於電子具有波粒二象性，其德布意波長可在原子尺寸的數量級以下，而且電子束可以用電場或磁場來聚焦，用電子束和電子透鏡取代光束和光學透鏡，發展起分辨本領比光學顯微鏡高得多的電子顯微鏡。

晶體的電子衍射

晶體對電子的衍射原理與晶體對x射線的衍射原理相同，都遵從勞厄方程，即衍射波相干條件為出射波矢時與入射波矢量之差等於晶體倒易矢量的整數倍

設倒易空間的基矢為，倒易矢量

在晶體中原子規則排成一層一層的平面，稱之為晶面，晶格倒易矢量的方向為晶面的法線方向，大小為晶面間距的倒數倍

為晶面指數（又稱密勒指數），它們是晶面與晶格平移基矢量的晶格坐標軸截距的約化整數，晶面指數表示晶面的取向，用來對晶面進行分類，標定衍射花樣。

晶格對電子波散射有彈性的，彈性散射波在空間相遇發生干涉形成衍射花樣，非彈性散射波則形成衍射花樣的背景襯度。入射波與晶格彈性散射，入射波矢量與出射波矢量大小相等，以波矢量大小為半徑，作一個球面，從球心向球面與倒易點陣的交點的射線為波的衍射線，這個球面稱為反射球（也稱厄瓦爾德球），見圖1所示，圖中的格點為晶格的倒易點陣（倒易空間點陣）。

晶格的電子衍射幾何以及電子衍射與晶體結構的關係由布拉格定律描述，兩層晶面上的原子反射的波相干加強的條件為

為衍射角的一半，稱為半衍射角。見圖2所示，圖中的格點為晶格點陣（正空間點陣）。o為衍射級，由於晶格對波的漫反射引起消光作用，的衍射一般都觀測不到。

電子衍射花樣與晶體結構

晶面間距不能連續變化，只能取某些離散值，例如，對於立方晶系的晶體，

a為晶格常數（晶格平移基矢量的長度），是包含晶體全部對稱性的、體積最小的晶體單元——單胞的一個棱邊的長度，圖3為立方晶系的三個布拉菲單胞。立方晶系單胞是立方體，沿hkl三個方向的棱邊長度相等，hkl三個晶面指數只能取整數；對於正方晶系的晶體

h,k,l三個方向相互垂直。h,k兩個方向的棱邊長度相等。三個晶面指數h,k,l只能取整數，只能取某些離散值，按照布拉格定律，只能在某些方向接收到衍射線。做單晶衍射時，在衍射屏或感光膠片上只能看到點狀分佈的衍射花樣，見圖4；做多晶衍射時，由於各個晶粒均勻地隨機取向，各晶粒中具有相同晶面指數的晶面的倒易矢在倒易空間各處均勻分佈形成倒易球面，倒易球面與反射球面相交為圓環，衍射線為反射球的球心到圓環的射線，射線到衍射屏或感光膠片上的投影呈環狀衍射花樣，見圖5。

衍射花樣的分佈規律由晶體的結構決定，並不是所有滿足布拉格定律的晶面都會有衍射線產生，這種現象稱為系統消光。若一個單胞中有n個原子，以單胞上一個頂點為坐標原點，單胞上第j個原子的位置矢量為，為晶格點陣的平移基矢量，第j個原子的散射波的振幅為為第j個原子的散射因子，根據勞厄方程，一個單胞中n個原子相干散射的複合波振幅。

根據正空間和倒易空間的矢量運算規則，。複合波振幅可寫為，上式中的求和與單胞中原子的坐標有關，單胞中n個原子相干散射的複合波振幅受晶體的結構影響，令。則單胞的衍射強度，稱為結構因子。

對於底心點陣，單胞中只有一個原子，其坐標為[0，0，0]，原子散射因子為，

任意晶面指數的晶面都能產生衍射。

對於底心點陣，單胞中有兩個原子，其坐標為[0，0，0]和，若兩個原子為同類原子，原子散射因子為，

只有當h,k同為偶數或同為奇數時，才不為0，h,k一個為偶數另為奇數時，為0，出現系統消光。

對於面心點陣，單胞中有4個原子，其坐標為[0，0，0]和，若4個原子為同類原子，原子散射因子為，只有為偶數時，不為0，能產生衍射。

對於面心點陣，單胞中有4個原子，其坐標為[0，0，0]和，若4個原子為同類原子，原子散射因子為，只有當h,k,l同為偶數可同為奇數時，才不為0，能產生衍射。

對於單胞中原子數目較多的晶體以及由異類原子所組成的晶體，還要引入附加系統消光條件。

電子衍射花樣的指數化

根據系統消光條件，可以確定衍射花樣的對應晶面的密勒指數hkl，這一步驟稱為衍射花樣的指數化。對衍射花樣指數化，可確定晶體結構，若已知電子波的波長，則可計算晶格常數，若已知晶格常數（由x射線衍射測定），則可計算電子波的波長，驗證德布羅意關係。以簡單格子立方晶系的多晶衍射花樣為例，介紹環狀衍射花樣的指數化。

對於電子衍射，電子波的波長很短，角一般只有，設衍射環的半徑為R，晶體到衍射屏或感光膠片的距離為L，由圖6所示的幾何關係可知，則布拉格定律為，（2）式中稱為儀器常數。，電子衍射花樣就是晶格倒易矢放大倍的象。將立方晶系的晶面間距代入布拉定律得。晶面指數h,k,l只能取整數，令，則各衍射環半徑平方的順序比為，按照系統消光規律，對於簡單立方、體心立方和面心立方晶格，半徑最小的衍射環對應的密勒指數分別為100、110、111，這三個密勒指數對應的晶面分別是簡單立方、體心立方和面心立方晶格中晶面間距最小的晶面。這三個晶格的衍射環半徑排列順序和對應的密勒指數見表1，將衍射環半徑的平方比表1對照，一般可確定衍射環的密勒指數。衍射花樣的指數化后，對已知晶格常數的晶體，儀器常數，(3)若已知儀器常數，則可計算晶格常數。