率失真理論
率失真理論
率失真理論是用資訊理論的基本觀點和方法研究數據壓縮問題的理論,又稱限失真信源編碼理論。率失真理論的基本問題可以歸結如下:對於一個給定的信源分佈與失真度量,在特定的碼率下能達到的最小期望失真;或者為了滿足一定的失真限制,最小描述碼率可以是多少。
率失真理論的名稱來源於信息速率失真函數,率失真理論包含兩個中心內容:一是率失真函數或失真率函數,二是限失真編碼定理。這就是針對不同的信源.不同的失真量度和不同信源概率分佈計算率失真函數和證明相應的限失真編碼定理。
率失真理論涉及三個基本概念;信源、編碼和失真量度。失真量度是這一理論特有的。它是對編解碼器輸入x和輸出y之間的失真所給予的量度,即d(x,y)。數學上,任何范數或距離(度量)都可作為失真量度。但在具體選擇時要考慮到物理上或主觀上應有意義,且數學上易處理和計算方便。已有的失真量度按量度的性質可分為范數失真量度和擬范數失真量度,按高階失真量度與一階失真量度的關係又可分為可加性量度和非可加性量度。現在常用的是差值失真量度和漢明失真量度。均方誤差失真量度,即d(x,y)=(x-y)2,既屬於范數失真量度,也屬於距離失真量度,又是一種差值失真量度,不僅有明確的物理意義,而且數學上也易於處理。
圖1
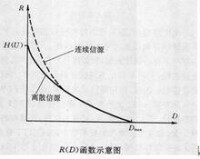
圖2
儘管這兩個函數的求解有一定難度,但這兩個函數變化的一般趨勢都很簡單。其中率失真函數R(D)是一個在(0,Dmax)區間上嚴格遞減、下凸的函數,D大於Dmax以後均取零。而在D=0時,對離散信源等於信源的熵,對連續信源則趨於無限大,如圖所示。失真率函數D(R)同樣是R的單調下降的下凸函數。
在最簡單的離散、無記憶、平穩信源和分組編況下,設信源的率失真函數是R(D),當R>R(D)時,一定存在一種具體的編碼方法,使其失真小於D+ε,其中ε是一個無窮小量。反之若R信源編碼定理就在數據壓縮的具體編碼方法和率失真函數之間建立起一種聯繫,對具體編碼方法的研究起到了指導作用。
率失真理論的主要應用有兩種:①數據壓縮。為數據壓縮的性能提供理論極限和比較標準,對具體編碼方法的研究起方向指導作用;②模式識別。統計模式識別與數據壓縮是兩個具有交叉領域的學科。率失真理論在模式分類、特徵選擇等問題上有重要的應用。
率失真理論在應用中,也存在一些問題。例如:它解決得較好的信源是平穩遍歷信源,而在實際中,信源經常是非平穩非遍歷的;它解決得比較好的編碼是分組碼,但在實際應用中,非分組碼相當普遍。同時,理論上要求對信源建立精確的模型,但實際上只能得到近似的模型;理論上假定已有正確的失真量度,但如何得到這量度尚無有效的辦法。
