共找到2條詞條名為芝諾悖論的結果 展開
- 物理學中的定理定律
- 飛矢不動悖論
芝諾悖論
物理學中的定理定律
芝諾悖論(Zeno's paradox)是古希臘數學家芝諾(Zeno of Elea)提出的一系列關於運動的不可分性的哲學悖論。

芝諾
柏拉圖在他的對話《巴門尼德篇》中,記載了芝諾和巴門尼德於公元前5世紀中葉去雅典的一次訪問。其中有這樣的文字:“巴門尼德年事已高,約65歲;頭髮很白,但儀錶堂堂。那時的芝諾約40歲,身材魁梧而美觀,大家說他已經變成巴門尼德所鍾愛的了。”在以後的希臘著作家看來,這次訪問是柏拉圖虛構的。但柏拉圖有關芝諾觀點的記敘,卻被普遍認為是準確的。
在柏拉圖的巴門尼德篇中,當芝諾談到自己的著作(論自然)時,這樣說道:“由於青年時的好勝著成此篇,著成后,人即將他竊去,以至我不能決斷,是否應當讓它問世。 ”芝諾不象他的老師那樣企圖從正面去證明是一不是多,是靜不是動,他常常從反面即歸謬法來為“存在論”辯護。公元五世紀的評論家普羅克洛斯(Proclus)說過,芝諾從“多”和運動的假設出發,一共推出了40個各不相同的悖論。現存的芝諾悖論至少有8個,其中關於運動的4個悖論最為著名。
芝諾的著作早已失傳,亞里士多德的物理學和辛普里西奧斯為物理學作的註解是了解芝諾悖論的主要途徑,此外只有少量零散的文獻可作參考。直到19 世紀中葉,亞里士多德關於芝諾悖論的引述及批評幾乎是權威的,人們普遍認為芝諾悖論不過是一些詭辯。英國數學家B.羅素感慨的說:“在這個變化無常的世界上,沒有什麼比死後的聲譽更變化無常了。死後得不到應有的評價的最典型例子莫過於埃利亞的芝諾了。他雖然發明了四個無限微妙無限深邃的悖論,後世的大批哲學家們卻宣稱他只不過是個聰明的騙子,而他的悖論只不過是一些詭辯。遭到兩千多年的連續駁斥之後這些詭辯才得以正名,…。”
19世紀下半葉以來,學者們開始重新研究芝諾。他們推測芝諾的理論在古代就沒能得到完整的、正確的報道,而是被詭辯家們用來倡導懷疑主義和否定知識,亞里士多德正是按照被詭辯家們歪曲過的形象來引述芝諾悖論的。學者們對芝諾提出這些悖論的目的還不清楚,但大家一致認為,芝諾關於運動的悖論不是簡單的否認運動,這些悖論後面有著更深的內涵。亞里士多德的著作保存了芝諾悖論的大意,從這個意義上來說,他功不可沒,但他對芝諾悖論的分析和批評是否成功,還不可以下定論。
有關芝諾悖論在古希臘數學發展中起到的作用,在科學史上眾說紛紜。P· 湯納利首先提出,不是巴門尼德而是畢達哥拉斯學派發現的不可公約量,對芝諾悖論的提出產生了深刻的影響。H·赫斯和H·斯科爾斯則認為芝諾是對古代數學的發展起決定影響的人物,他們試圖證明,畢達哥拉斯學派曾假定存在無限小的基本線段,想以此來克服因發現不可公約量而引起的矛盾,而芝諾的悖論反對了這種不準確的做法,從而迫使其他數學家去尋找真正的原因所在。另有一些學者持有完全不同的觀點,他們認為芝諾對那個時代的數學發展沒有作出任何重大的貢獻。
不管爭論的結果如何,人們無須擔心芝諾的名字會從數學史上消失,就像美國數學史家E·T·貝爾說的,芝諾畢竟曾“以非數學的語言,記錄下了最早同連續性和無限性格鬥的人們所遭遇到的困難。”芝諾的功績在於把動和靜的關係、無限和有限的關係、連續和離散的關係惹人注意地擺了出來,並進行了辨證的考察。在哲學上,芝諾被亞里士多德譽為辯證法的發明人,黑格爾在他的哲學史演錄中指出:“芝諾主要是客觀的辨證的考察了運動,並稱芝諾為‘辯證法的創始人’”。
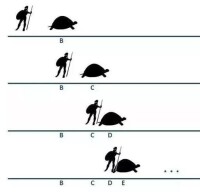
芝諾悖論示意圖
芝諾:“一個人從A點走到B點,要先走完路程的1/2,再走完剩下總路程的1/2,再走完剩下的1/2……”如此循環下去,永遠不能到終點。
假設此人速度不變,走一段的時間每次除以2,時間為實際需要時間的1/2+1/4+1/8+......,則時間限制在實際需要時間以內,即此人與目的地距離可以為任意小,卻到不了。實際上是這個悖論本身限定了時間,當然到達不了。
《莊子·天下篇》中也提到:“一尺之棰,日取其半,萬世不竭。”
芝諾與莊子悖論的區別為芝諾悖論一定時間內行走的距離不變(即速度不變),而莊子時間不變,這段時間裡的工作卻越來越少(速度越來越慢),可以看出芝諾限制了時間,而莊子的理論可以使時間為無窮大。
阿基里斯(又名阿喀琉斯)是古希臘神話中善跑的英雄。在他和烏龜的競賽中,他速度為烏龜十倍,烏龜在前面100米跑,他在後面追,但他不可能追上烏龜。因為在競賽中,追者首先必須到達被追者的出發點,當阿喀琉斯追到100米時,烏龜已經又向前爬了10米,於是,一個新的起點產生了;阿喀琉斯必須繼續追,而當他追到烏龜爬的這10米時,烏龜又已經向前爬了1米,阿喀琉斯只能再追向那個1米。就這樣,烏龜會製造出無窮個起點,它總能在起點與自己之間製造出一個距離,不管這個距離有多小,但只要烏龜不停地奮力向前爬,阿喀琉斯就永遠也追不上烏龜!
“烏龜”動得最慢的物體不會被動得最快的物體追上。由於追趕者首先應該達到被追者出發之點,此時被追者已經往前走了一段距離。因此被追者總是在追趕者前面。”
如柏拉圖描述,芝諾說這樣的悖論,是興之所至的小玩笑。首先,巴門尼德編出這個悖論,用來嘲笑"數學派"所代表的畢達哥拉斯的" 1-0.999...>0"思想。然後,他又用這個悖論,嘲笑他的學生芝諾的"1-0.999...=0,但1-0.999...>0"思想。最後,芝諾用這個悖論,反過來嘲笑巴門尼德的"1-0.999...=0,或1-0.999...>0"思想。
有人解釋道:若慢跑者在快跑者前一段,則快跑者永遠趕不上慢跑者,因為追趕者必須首先跑到被追者的出發點,而當他到達被追者的出發點,慢跑者又向前了一段,又有新的出發點在等著它,有無限個這樣的出發點。
芝諾當然知道阿喀琉斯能夠捉住海龜,跑步者肯定也能跑到終點。
類似阿基里斯追上海龜之類的追趕問題,我們可以用無窮數列的求和,或者簡單建立起一個方程組就能算出所需要的時間,那麼既然我們都算出了追趕所花的時間,我們還有什麼理由說阿基里斯永遠也追不上烏龜呢?然而問題出在這裡:我們在這裡有一個假定,那就是假定阿基里斯最終是追上了烏龜,才求出的那個時間。但是芝諾的悖論的實質在於要求我們證明為何能追上。上面說到無窮個步驟是難以完成。
以上初等數學的解決辦法,是從結果推往過程的。悖論本身的邏輯並沒有錯,它之所以與實際相差甚遠,在於這個芝諾與我們採取了不同的時間系統。人們習慣於將運動看做時間的連續函數,而芝諾的解釋則採取了離散的時間系統。即無論將時間間隔取得再小,整個時間軸仍是由無限的時間點組成的。換句話說,連續時間是離散時間將時間間隔取為無窮小的極限。
其實這歸根到底是一個時間的問題。譬如說,阿基里斯速度是10m/s,烏龜速度是1m/s,烏龜在前面100m。實際情況是阿基里斯必然會在100/9秒之後追上烏龜。按照悖論的邏輯,這100/9秒可以無限細分,給我們一種好像永遠也過不完的印象。但其實根本不是如此。這就類似於有1秒時間,我們先要過一半即1/2秒,再過一半即1/4秒,再過一半即1/8秒,這樣下去我們永遠都過不完這1秒,因為無論時間再短也可無限細分。但其實我們真的就永遠也過不完這1秒了嗎?顯然不是。儘管看上去我們要過1/2、1/4、1/8秒等等,好像永遠無窮無盡。但其實時間的流動是勻速的,1/2、1/4、1/8秒,時間越來越短,看上去無窮無盡,其實加起來只是個常數而已,也就是1秒。所以說,芝諾的悖論是不存在的。
設想一支飛行的箭。在每一時刻,它位於空間中的一個特定位置。由於時刻無持續時間,箭在每個時刻都沒有時間而只能是靜止的。鑒於整個運動期間只包含時刻,而每個時刻又只有靜止的箭,所以芝諾斷定,飛行的箭總是靜止的,它不可能在運動。
上述結論也適用於時刻有持續時間的情況。對於這種情況,時刻將是時間的最小單元。假設箭在這樣一個時刻中運動了,那麼它將在這個時刻的開始和結束位於空間的不同位置。這說明時刻具有一個起點和一個終點,從而至少包含兩部分。但這明顯與時刻是時間的最小單元這一前提相矛盾。因此,即使時刻有持續時間,飛行的箭也不可能在運動。總之,飛矢不動。
箭悖論的標準解決方案如下:箭在每個時刻都不動這一事實不能說明它是靜止的。運動與時刻里發生什麼無關,而是與時刻間發生什麼有關。如果一個物體在相鄰時刻在相同的位置,那麼我們說它是靜止的,反之它就是運動的。
首先假設在操場上,在一瞬間(一個最小時間單位)里,相對於觀眾席A,列隊B、C將分別各向右和左移動一個距離單位。
◆◆◆◆觀眾席A
▲▲▲▲隊列B
▼▼▼▼隊列C
B、C兩個列隊開始移動,如下圖所示相對於觀眾席A,B和C分別向右和左各移動了一個距離單位。
◆◆◆◆觀眾席A
▲▲▲▲隊列B……向右移動
▼▼▼▼隊列C……向左移動
而此時,對B而言C移動了兩個距離單位。也就是,隊列既可以在一瞬間(一個最小時間單位)里移動一個距離單位,也可以在半個最小時間單位里移動一個距離單位,這就產生了半個時間單位等於一個時間單位的矛盾。因此隊列是移動不了的。
運動場問題是芝諾提出的四個悖論中的第一個,又稱為兩分法悖論
畢達哥拉斯學派
其結論為:運動不可能開始。
其論點為:因為一運動物體在到達目的地之前,必須先抵達距離目的地之一半的位置。即:若要從A處到達B處,必須先到AB中點C,要到達C,又須先到達AC的中點D。如此繼續劃分下去,所謂的“一半距離”數值將越來越小。最後“一半距離”幾乎可被視為零。這就形成了此一物體若要從A移動到B,必須先停留在A的悖論。這樣一來,此物體將永遠停留在初始位置(或者說物體初始運動所經過的距離近似0),以至這物體的運動幾乎不能開始。即:由於運動的物體在到達目的地前必須到達其半路上的點,若假設空間無限可分則有限距離包括無窮多點,於是運動的物體會在有限時間內經過無限多點。
