張量分析
數學術語之一
目錄
個分微分幾何中研究張量場的微分運算的一支。它提供了微分幾何研究中的一種重要工具。黎曼幾何就是在張量分析的基礎上發展起來的。
在了解了張量的定義及其代數運算后,人們自然地要對張量場的微分進行研究。然而,將(r,s)型張量場在局部坐標系下的分量求導后一般並不能得到一個(r,s+1)型張量場。為了能得到一個(r,s+1)型張量場,就必須在普通導數的基礎上加上一定的補償項。設 (r,s)型張量場K的分量為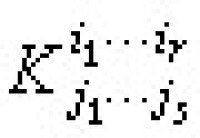 ,令
,令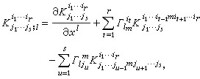
張量分析
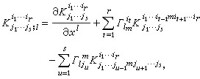
張量分析
於是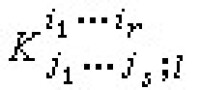 滿足(r,s+1)型張量的變換規則
滿足(r,s+1)型張量的變換規則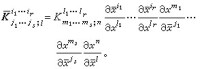
張量分析
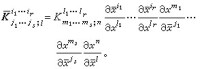
張量分析
也把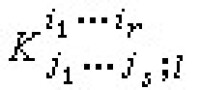 記為,因此墷l是一個運算元,它把(r,s)型張量場K變成一個(r,s+1)型張量場墷K,稱墷K為張量場K的協變微分,稱墷lK為K關於變數xl 的協變導數。例如,對反變向量(即一階反變張量)場
記為,因此墷l是一個運算元,它把(r,s)型張量場K變成一個(r,s+1)型張量場墷K,稱墷K為張量場K的協變微分,稱墷lK為K關於變數xl 的協變導數。例如,對反變向量(即一階反變張量)場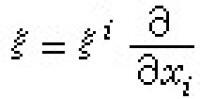 ,
,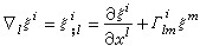 ,
,
張量分析
張量分析
張量分析
對協變向量場(即一階協變張量場),,
對一階反變、一階協變張量場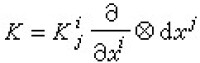 ,
,
張量分析
一般地說,運算元墷k與墷l不可交換,墷k墷l與墷l墷k的差與聯絡的曲率、撓率有關。由此可導出一系列有用的恆等式,如里奇恆等式等,這些恆等式及各種協變導數之間的相互關係就形成了張量分析的主要內容。例如當ƒ,ξ,α分別為數量場、反變向量場及協變向量場時,它們滿足下列關係:
張量分析
式中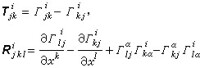
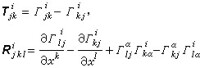
張量分析
分別是聯絡Г 的撓率張量和曲率張量。特別,當撓率為零時,有
的撓率張量和曲率張量。特別,當撓率為零時,有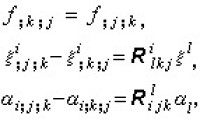
張量分析
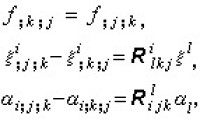
張量分析
稱這些公式為里奇恆等式。
微分幾何中一些重要的微分運算元在局部坐標系下可用協變導數表達出來。如向量場的散度為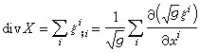 ,
,
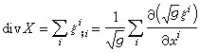
張量分析
式中g=det(gij)。如α為p形式,則α 的外微分dα及伴隨外微分δα分別為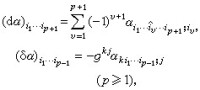
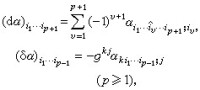
張量分析
式中“∧”表示缺掉相應的指標。因而拉普拉斯運算元Δ=dδ+δd的表示式為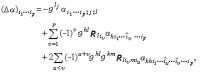
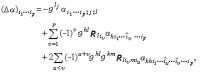
張量分析
式中。當p=0時,即對數量場ƒ,有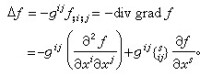
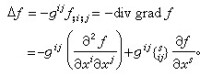
張量分析
作用在數量場ƒ上的運算元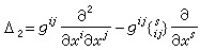
張量分析
稱為第二類貝爾特拉米微分運算元。有Δ2ƒ=-Δƒ。作用在數量場ƒ上的第一類貝爾特拉米微分運算元Δ1為。
