圖像去噪
減少數字圖像雜訊的過程
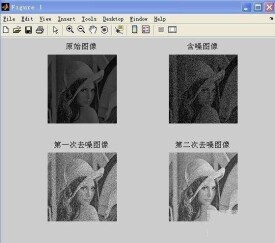
圖像去噪是指減少數字圖像中雜訊的過程稱為圖像去噪。現實中的數字圖像在數字化和傳輸過程中常受到成像設備與外部環境雜訊干擾等影響,稱為含噪圖像或雜訊圖像。
雜訊是圖象干擾的重要原因。一幅圖象在實際應用中可能存在各種各樣的雜訊,這些雜訊可能在傳輸中產生,也可能在量化等處理中產生。
根據雜訊和信號的關係可將其分為三種形式:(f(x,y)表示給定原始圖象,g(x,y)表示圖象信號,n(x,y)表示雜訊。
2) 乘性雜訊,此類雜訊與圖象信號有關,含噪圖象可表示為f(x,y)=g(x,y)+n(x,y)g(x,y),飛點掃描器掃描圖象時的雜訊,電視圖象中的相關雜訊,膠片中的顆粒雜訊就屬於此類雜訊;
3) 量化雜訊,此類雜訊與輸入圖象信號無關,是量化過程存在量化誤差,再反映到接收端而產生。
採用鄰域平均法的均值濾波器非常適用於去除通過掃描得到的圖像中的顆粒雜訊。領域平均法有力地抑制了雜訊,同時也由於平均而引起了模糊現象,模糊程度與領域半徑成正比。
幾何均值濾波器所達到的平滑度可以與算術均值濾波器相比,但在濾波過程中會丟失更少的圖象細節。
它能根據圖象的局部方差來調整濾波器的輸出,局部方差越大,濾波器的平滑作用越強。它的最終目標是使恢復圖像f^(x,y)與原始圖像f(x,y)的均方誤差e2=E[(f(x,y)-f^(x,y)2]最小。該方法的濾波效果比均值濾波器效果要好,對保留圖像的邊緣和其他高頻部分很有用,不過計算量較大。維納濾波器對具有白雜訊的圖象濾波效果最佳。
它是一種常用的非線性平滑濾波器,其基本原理是把數字圖像或數字序列中一點的值用該點的一個領域中各點值的中值代換其主要功能是讓周圍象素灰度值的差比較大的像素改取與周圍的像素值接近的值,從而可以消除孤立的雜訊點,所以中值濾波對於濾除圖像的椒鹽雜訊非常有效。中值濾波器可以做到既去除雜訊又能保護圖像的邊緣,從而獲得較滿意的復原效果,而且,在實際運算過程中不需要圖象的統計特性,這也帶來不少方便,但對一些細節多,特別是點、線、尖頂細節較多的圖象不宜採用中值濾波的方法。
將開啟和閉合結合起來可用來濾除雜訊,首先對有雜訊圖象進行開啟操作,可選擇結構要素矩陣比雜訊的尺寸大,因而開啟的結果是將背景上的雜訊去除。最後是對前一步得到的圖象進行閉合操作,將圖象上的雜訊去掉。根據此方法的特點可以知道,此方法適用的圖像類型是圖象中的對象尺寸都比較大,且沒有細小的細節,對這種類型的圖像除噪的效果會比較好。