高斯單位制
計量單位的制度
高斯單位制(Gaussian units)是一種計量單位的制度,屬於公制,是從厘米-克-秒制衍生,電磁單位系統中最常見的一種單位制。在厘米-克-秒制內,又有幾組互相衝突的電磁單位,不單隻存在有高斯單位。所以,使用術語“厘米-克-秒單位”很可能會引起分歧義,必需盡量避免。
高斯單位制(CGS),又稱混合單位制,又稱厘米克秒制(centimetre-gram-second system),簡稱高斯制。高斯制在電磁學中有兩套單位制,一套以庫侖定律為基礎,稱為靜電制,記作CGSE;另一套以安培定律為基礎,成為靜磁制,記作CGSM。在高斯單位制中,與點電荷有關的公式都很簡單,在實際應用中比較方便,所以有些書刊仍然採用高斯單位制。
除了高斯單位制以外,最常用的別種選擇是國際單位制。在大多述領域,國際單位制是主要使用的單位制。隨著時光的流易,越來越多的人士選擇摒棄高斯單位制,改採用國際單位制。高斯單位制與國際單位制之間的單位轉換並不像平常單位轉換那樣簡易。例如,電磁學的物理定律方程,像麥克斯韋方程組,依使用哪種單位制而定,需要做相關調整;在高斯單位制是無量綱的物理量,像電容率或磁導率,換到國際單位制,可能會變為具有量綱。
目前,高斯單位制必須與國際單位制掛鉤才有實驗意義,因為只有國際單位制才對各個物理量有精確的定義。高斯單位制在某些領域會使公式較為簡潔,例如經常需要處理球對稱情況的天體物理學領域。但在經常需要處理直線情況的工程領域,國際單位制的公式更加簡潔。
基本單位如右圖。

高斯單位制
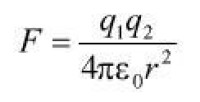
國際制中的庫侖定律
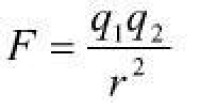
靜電制中的庫侖定律
靜磁學中的安培定律在國際制和靜磁製中的表達式也是不同的。安培定律描述兩根相距r,攜帶電流的導線之間的相互作用力。表達式如下。

安培定律
最後列表總結。
 高斯單位制 |
| 電磁學物理量 |
在厘米-克-秒制內,有好幾種電磁單位系統,高斯單位制只是其中的一種。其它有靜電單位制(electrostatic units)、電磁單位制(electromagnetic units)、洛倫茲-亥維賽單位制(Lorentz-Heaviside units)。
另外還有一類稱為自然單位制的制度,包括原子單位制、普朗克單位制等等。從某些方面來看,在厘米-克-秒制與國際單位制之間,這些自然單位制比較接近前者。例如,假設選擇自然單位制或厘米-克-秒制,則高斯定律方程里,都有一個因子,而庫侖定律方程里則無;假設選擇國際單位制,則高斯定律方程里沒有因子,而庫侖定律方程里則有。另外,高斯單位制比國際單位制少一個基本單位,即電荷的單位不是基本單位,而自然單位制的基本單位又少了許多。
現今,國際單位制是最常使用的單位制。在工程學領域與實用領域,幾乎普遍採用國際單位制,這已是很多年的事實。在科技文獻里,像理論物理學與天文學的文獻,直到最近幾年,高斯單位制是主要單位制,但現在也越來越少使用。
自然單位制比較常見於更理論、更抽象的物理領域,特別是粒子物理學與弦理論。
有理化單位制
高斯單位制與國際單位制之間,一個差別是在一些方程里的因子4π。國際單位制被分類為“有理化單位制”,因為,麥克斯韋方程組裡沒有因子4π,但是,庫侖定律和畢奧-薩伐爾定律的方程里,都含有因子4π。採用高斯單位制的狀況完全相反。麥克斯韋方程組裡含有因子4π,但是,庫侖定律和畢奧-薩伐爾定律的方程里,都沒有因子4π。因此,高斯單位制被分類為“非理化單位制”。
電荷的單位
對於高斯單位制與國際單位制,電荷單位的定義有很大的區別。國際單位制特別為電現象設置一個基本單位──安培(ampere),這動作的後果是,電荷是一種物理數量的一種獨特量綱,(1庫倫(coulomb)=1ampere×1second)不能用機械單位(kg、m、s)來表達。庫侖定律方程為
其中,F是庫侖力,是真空介電常數,Q1和Q2是兩個相互作用的電荷,r是這兩個電荷之間的距離。
在高斯單位制內,電荷的單位statC,可以完全以機械單位寫為1 statC = 1 gcms
庫侖定律方程相當簡單:
假設電荷的單位是statC,半徑的單位是cm,則作用力的單位是達因(dyne)。
磁物理量的單位
與國際單位制不同,在高斯單位制內,電場E與磁感應強度(B場)B的量綱一樣。這總計為B場在兩個單位制內光速因子c的差異。同樣的因子也發生於其他磁物理量,像磁場強度(H場)與磁化強度。例如,對於傳播於真空的平面電磁波,在高斯單位制內, ;但在國際單位制內, 。
電極化矢量、磁化矢量