坐標變換
坐標變換
採用一定的數學方法將一種坐標系的坐標變換為另一種坐標系的坐標的過程。寫3d圖形程序,就一定會做坐標變換。而談到坐標變換,就不得不提起投影變換,因為它是所有變換中最不容易弄懂的。但有趣的是,各種關於透視變換的文檔卻依然是簡之又簡,甚至還有前後矛盾的地方。看來如此這般光景,想要弄清楚它,非得自己動手不可了。所以在下面的文章里,作者嘗試推導一遍這個難纏的透視變換,然後把它套用到 DX和 PS2lib 的實例中去。
共有五種,除平移外均以坐標原點為基準點,即變換前後坐標原點不變。
下面給出五種基本變換的中英文名稱和矩陣描述。
以逆時針旋轉為例。則舊坐標到新坐標的變換矩陣為
繞Z軸.................................繞Y軸................................繞X軸
反射變換的實質是負變倍,實際上叫做“鏡像”更為貼切。
基於X軸..............基於Y軸
基於Y-X平面............基於X-Z平面............基於Z-Y平面
基於任意平面的坐標變換
只要將其看成兩個線性空間的映射即可
坐標變換
由於直流電機的主磁通基本上唯一地由勵磁繞組的勵磁電流決定,所以這是直流電機的數學模型及其控制系統比較簡單的根本原因。
如果能將交流電機的物理模型等效地變換成類似直流電機的模式,分析和控制就可以大大簡化。坐標變換正是按照這條思路進行的。
不同電機模型彼此等效的原則是:在不同坐標下所產生的磁動勢完全一致。
1.坐標變換原理
產生的合成磁動勢是旋轉磁動勢F,它在空間呈正弦分佈,以同步轉速ws(即電流的角頻率)順著的相序旋轉。這樣的物理模型繪於下圖1中。
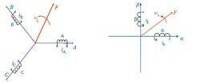
坐標變換
旋轉磁動勢並不一定非要三相不可,除單相以外,二相、三相、四相、…… 等任意對稱的多相繞組,通以平衡的多相電流,都能產生旋轉磁動勢,當然以兩相最為簡單。
圖2中繪出了兩相靜止繞組a和b它們在空間互差90°,通以時間上互差90°的兩相平衡交流電流,也產生旋轉磁動勢F。
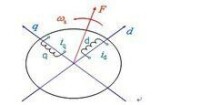
坐標變換
圖3旋轉的直流繞組
圖3兩個匝數相等且互相垂直的繞組d 和q,其中分別通以直流電流id和iq,產生合成磁動勢F,其位置相對於繞組來說是固定的。如果讓包含兩個繞組在內的整個鐵心以同步轉速旋轉,則磁動勢F自然也隨之旋轉起來,成為旋轉磁動勢。
把這個旋轉磁動勢的大小和轉速也控制成與圖1 和圖2中的磁動勢一樣,那麼這套旋轉的直流繞組也就和前面兩套固定的交流繞組都等效了。
由此可見,以產生同樣的旋轉磁動勢為準則,圖1的三相交流繞組、圖2的兩相交流繞組和圖3中整體旋轉的直流繞組彼此等效。或者說,在三相坐標系下的,在兩相坐標系下的和在旋轉兩相坐標系下的直流是等效的,它們能產生相同的旋轉磁動勢。
坐標變換的任務就是求出 之間準確的等效關係。
2.三相--兩相變換(變換)
在三相靜止繞組和兩相靜止繞組之間的變換,或稱三相靜止坐標系和兩相靜止坐標系間的變換,簡稱 變換。
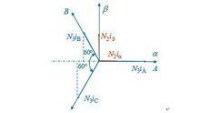
坐標變換
上圖繪出了兩個坐標系,為方便起見,取A軸和a軸重合。設三相繞組每相有效匝數為,兩相繞組每相有效匝數為,各相磁動勢為有效匝數與電流的乘積,其空間矢量均位於有關相的坐標軸上。由於交流磁動勢的大小隨時間在變化著,圖中磁動勢矢量的長度是隨意的。
設磁動勢波形是正弦分佈的,當三相總磁動勢與二相總磁動勢相等時,兩套繞組瞬時磁動勢在a、b軸上的投影都應相等,
寫成矩陣形式,得
考慮變換前後總功率不變,在此前提下匝數比應為
代入上式,得
三相—兩相坐標系的變換矩陣
令 表示從三相坐標系變換到兩相坐標系的變換矩陣,則
3.兩相—兩相旋轉變換(變換)
從兩相靜止坐標繫到兩相旋轉坐標系d、q 變換稱作兩相—兩相旋轉變換,簡稱2s/2r 變換,其中s 表示靜止,r 表示旋轉。
圖5兩相靜止和旋轉坐標系與磁動勢(電流)空間矢量
兩相交流電流ia、ib和兩個直流電流id、iq 產生同樣的以同步轉速ws旋轉的合成磁動勢Fs。由於各繞組匝數都相等,可以消去磁動勢中的匝數,直接用電流表示,例如Fs可以直接標成is。但必須注意,這裡的電流都是空間矢量,而不是時間相量。
d,q軸和矢量Fs(is )都以轉速ws 旋轉,分量的長短不變,相當於d,q繞組的直流磁動勢。但a、b軸是靜止的,a軸與d軸的夾角j隨時間而變化,因此is 在a、b軸上的分量的長短也隨時間變化,相當於繞組交流磁動勢的瞬時值。由圖5可見,之間存在下列關係
變換公式
兩相旋轉—兩相靜止坐標系的變換矩陣寫成矩陣形式,得式中
是兩相旋轉坐標系變換到兩相靜止坐標系的變換陣。
任意兩空間坐標系的轉換由於測量坐標系和施工坐標系採用不同的標準,要進行精確轉換,必須知道至少3個重合點(即為在兩坐標系中坐標均為已知的點。採用布爾莎模型進行求解。布爾莎公式:對該公式進行變換等價得到:解算這七個參數,至少要用到三個已知點(2個坐標系統的坐標都知道),採用間接平差模型進行解算:其中: V 為殘差矩陣; X 為未知七參數; A 為係數矩陣; 解之:L 為閉合差解得七參數后,利用布爾莎公式就可以進行未知點的坐標轉換了,每輸入一組坐標值,就能求出它在新坐標系中的坐標。但是要想GPS觀測成果用於工程或者測繪,還需要將地方直角坐標轉換為大地坐標,最後還要轉換為平面高斯坐標。上述方法類同於我們的間接平差,解算起來較複雜,以下提供坐標轉換程序,只需輸入三個已知點的坐標即可求解出坐標轉換的七個參數。如果已知點的數量較多,可以進行參數間的平差運算,則精度更高。當已知點的數量只有兩個時,我們可以採用簡單變換法,此法較為方便易行,適於手算,只是精度受到一定的限制。詳細解算方程如下:式中調x,y和x\'、y\'分別為新舊(或;舊新)網重合點的坐標,a、b、、k為變換參數,顯然要解算出a、b、、k,必須至少有兩個重合點,列出四個方程。即可進行通常的參數平差,解求a、x、b、c、d各參數值。將之代人(3)式,可得各擬合點的殘差(改正數)代人(2)式,可得待換點的坐標。求出解算參數之後,可在Excel中,進行其餘坐標的轉換。上次筆者用此法進行過80和54坐標的轉換,由於當時沒有多餘的點可供驗證和平差,所以轉換精度不得而知,但轉換之後各點的相對位置不變。估計,實際的轉換誤差應該是10m量級的。還有一些情況是先將大地坐標轉換 為直角坐標,然後進行相關轉換