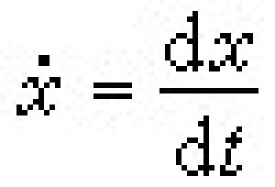狀態空間法

狀態空間法（state-space techniques ）是現代控制理論中建立在狀態變數描述基礎上的對控制系統分析和綜合的方法。狀態變數是能完全描述系統運動的一組變數。如果系統的外輸入為已知，那麼由這組變數的現時值就能完全確定系統在未來各時刻的運動狀態。通過狀態變數描述能建立系統內部狀態變數與外部輸入變數和輸出變數之間的關係。反映狀態變數與輸入變數間因果關係的數學描述稱為狀態方程，而輸出變數與狀態變數和輸入變數間的變換關係則由量測方程來描述。狀態與狀態變數描述的概念早就存在於經典動力學和其他一些領域，但將它系統地應用於控制系統的研究，則是從1960年R.E.卡爾曼發表《控制系統的一般理論》的論文開始的。狀態空間法的引入促成了現代控制理論的建立。

狀態空間法的主要數學基礎是線性代數。在狀態空間法中，廣泛用向量來表示系統的各種變數組，其中包括狀態向量、輸入向量和輸出向量。變數的個數規定為相應向量的維數。用x表示系統的狀態向量，用u和y分別表示系統的輸入向量和輸出向量，則系統的狀態方程和量測方程可表示為如下的一般形式：

x'=f(x，u，t)，　y=g(x，u，t)

式中,f(x，u，t)和g(x，u，t)為自變數x、u、t的非線性向量函數,t為時間變數。對於線性定常系統狀態方程和量測方程具有較為簡單的形式：

x'=Ax+Bu， y=Cx+Du

式中A為系統矩陣，B為輸入矩陣，C為輸出矩陣,D為直接傳遞矩陣，它們是由系統的結構和參數所定出的常數矩陣。在狀態空間法中，控制系統的分析問題常歸結為求解系統的狀態方程和研究狀態方程解的性質。這種分析是在狀態空間中進行的。所謂狀態空間就是以狀態變數為坐標軸所構成的一個多維空間。狀態向量隨時間的變化在狀態空間中形成一條軌跡。對於線性定常系統，狀態軌跡主要由系統的特徵值決定。系統的特徵值規定為系統矩陣A的特徵方程det(sI-A)=0的根，其特徵可由它在s複數平面上的分佈來表徵。當運用狀態空間法來綜合控制系統時，問題就變為選擇一個合適的輸入向量，使得狀態軌跡滿足指定的性能要求。

狀態空間法有很多優點。由於採用矩陣表示，當狀態變數、輸入變數或輸出變數的數目增加時，並不增加系統描述的複雜性。狀態空間法是時間域方法，所以很適合於用數字電子計算機來計算。狀態空間法能揭示系統內部變數和外部變數間的關係，因而有可能找出過去未被認識的系統的許多重要特性，其中能控性和能觀測性尤其具有特別重要的意義。研究表明，從系統的結構角度來看，狀態變數描述比經典控制理論中廣為應用的輸入輸出描述（如傳遞函數）更為全面。

狀態空間法的運用對現代控制理論中其他各種方法的發展起了重要的推動作用。線性系統代數理論、線性系統幾何理論和多變數頻域方法，都是在狀態空間法的影響下發展起來的。