多變數頻域方法

線性系統理論中建立在頻率域分析基礎上的一個理論分支，是用多項式矩陣理論把狀態空間方法同經典頻率域方法結合起來，研究線性定常多變數控制系統的一整套理論和設計方法。這種方法直接考察系統諸變數間各種運算的相互關係，把問題歸結為相應運算元的有理分式矩陣的研究。在連續時間情形下，這些運算元是普通的微分運算元，經過拉普拉斯變換后就變成普通的複數並具有復頻率的物理含義。因此這種方法本質上是一種頻率域方法。

經典的頻率域方法採用傳遞函數、頻率響應等描述系統輸入輸出關係的特性，對用於解決單變數控制系統的設計問題很方便。1960年前後興起的現代控制理論以狀態空間法（即時間域方法）作為主要的分析和綜合方法，它能描述多變數系統的內部結構，而且適於應用計算機進行分析和設計。但狀態空間法在處理複雜的工業過程式控制制時遇到了困難，主要表現在：①難以獲得被控對象的精確數學模型；②難以用明顯形式規定被控對象行為的性能指標；③直接採用最優控制和最優濾波（見卡爾曼-布希濾波）綜合得到的控制器的結構過於複雜，在技術上很難實現。70年代中，H.H.羅森布羅克等人創立了多變數頻域方法，成為現代線性系統理論中有影響的學派之一。多變數頻域方法能全面反映系統的內部特性，揭示由時間域方法所導出的各種概念和規律，同時還具有經典頻率域方法的集約程度高、物理概念清晰和便於對控制系統進行設計調整等優點。

在多變數頻域方法中，線性定常系統的數學模型通常採用以部分主要狀態變數（稱為分狀態）z(t)代表系統行為的微分運算元描述：

T(S)Z＝U(S)u

y＝V(S)Z＋W(S)u

式中u為輸入即控制向量,y為輸出向量。T(S)、U(S)、V(S)、W(S)都是以s(微分運算元或拉普拉斯變換運算元)為自變數的多項式矩陣，它們能提供描述系統所需的全部信息。因此，如下構成的分塊矩陣被稱為系統矩陣：

系統的許多內部特性都可通過對系統矩陣的分析而得到。例如，T(S)和U(S)的左互質（它們的左乘公因式矩陣的行列式為非零常數）表示系統的能控性，T(S)和V(S)的右互質則表示系統的能觀測性。系統的傳遞函數矩陣 G(S)與系統矩陣間的關係為

G(S)＝V(S)T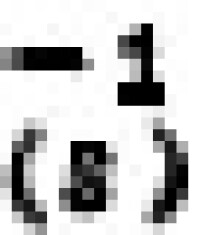U(S)+W(S)

式中T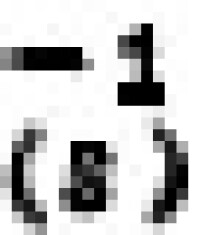是T(S)的逆矩陣。在多變數頻域方法中還常採用系統的矩陣分式描述(簡記為MFD)，即按照一定條件把G(S)分解成兩個多項式矩陣相除的形式：Nr(S)D峊或D屢N1(S)。前者稱為右MFD，後者稱為左MFD。採用系統的矩陣分式描述，可以方便地應用多項式矩陣理論對系統進行分析和設計。多變數系統的輸入輸出特性同傳遞函數的極點（在D(S)和N(S)為互質時，代數方程detD(S)=0的根）和零點（在D(S)和N(S)為互質時，使N(S)秩的s值）之間具有密切的關係。

多變數系統基於頻率響應的設計方法有逆奈奎斯特陣列方法、序列回差方法、並矢展開方法和特徵軌跡方法等。這些方法的共同特點是，把多輸入、多輸出且迴路間緊密關聯的多變數系統的設計問題，化為一系列單變數系統的設計問題，進而可以選用某一種經典方法（例如頻率響應法、根軌跡法）完成系統的設計。這些方法需要經過複雜的計算和採用計算機輔助設計和模擬，以及通過人機對話反覆修改後才能得到滿意的結果。利用帶有圖形顯示終端的人機對話式計算機輔助設計，能充分發揮設計者的經驗和知識，設計出滿足品質要求、結構簡單的控制器。基於多變數頻域方法的控制系統計算機輔助設計程序包已經得到廣泛應用。

多變數頻域方法已比較成功地應用於石油、化工、造紙、原子能反應堆、自動駕駛儀等領域的控制系統的設計。

參考書目

H.H.Rosenbrock， State Space and Multivariable Theory, Nelson, London,1970.

H.H.Rosenbrock，Computer-aided Control System Design, Academic Press,London,1974.

A.G.J.MacFarlane ed., Complex Variable Methodsfor Linear Multivariable Feedback Systems, Taylorand Francis Ltd.,London,1980.