奇點分佈法
奇點分佈法
奇點分佈法是解無粘性不可壓縮流體無旋運動的問題的一個重要方法。
目錄
無粘性不可壓縮流體無旋運動和具有單值導數的調和函數之間存在著一一對應關係,即任何一個無旋運動都存在著相應的調和函數──速度勢ф與之對應。反過來,給定一個具有單值導數的調和函數,將它看作某無旋運動的速度勢函數,則得一無旋運動與之對應。奇點分佈法的主要思想可簡述如下:首先建立簡單的、對應於均勻流、源流、匯流、點渦、偶極子流等基本流子的調和函數,而後將這些基本的調和函數──速度勢以適當的方式疊加起來,疊加后所得的仍為調和函數。利用這些新得到的調和函數可以解決兩類問題。第一類稱為正問題,即給定物體求物體繞流問題的解。為此目的,適當地選擇基本流子的組合,使得複合后所得調和函數滿足給定的邊界條件。第二類稱為反問題,即給出速度勢函數,反過來確定與之對應的無旋運動。利用奇點分佈法解決這類問題時只須根據一定的物理考慮,將基本流子疊加起來,而後研究並確定它代表什麼樣的無旋運動。奇點分佈法的優點是簡便,物理概念清晰,利用它可以解決一批工程實際感興趣的無粘性不可壓縮流體無旋運動問題。
以平面運動作為例子。此時用複位勢代替速度勢較為方便。均勻流、源流、匯流、點渦和偶極子流等基本流子的複位勢分別為:
(1)
式中堸∞、Q、Γ分別為無窮遠處共軛速度、點源強度、速度環量;Μ=meiβ為偶極子矩,其中m為偶極子矩的大小,β為匯到源的方向角。下面分別用圓柱繞流問題和薄翼繞流問題說明如何用奇點分佈法解反問題和正問題。
圓柱繞流問題 用它說明如何應用奇點分佈法解反問題。設一細長物體沿長軸方向等速向左運動,流體在物體前端不斷受擠壓,而在尾后讓出來的空間里又匯合起來(圖1)。這樣物體的運動狀態就類似於前端有個點源,後端有個點匯。現在設想細長體前緣的曲率中心逐漸靠近后緣的曲率中心,當兩者重合時就得到圓柱體。這時前端的點源和後端的點匯也重合在一起變成偶極子,偶極子的方向恰好和來流方向相反。有理由預測,圓柱定常繞流問題的解可能由下列兩個基本流子疊加起來得到:①沿x軸速度為V∞的均勻流;②原點處矩為m、軸線方向與來流方向相反的偶極子流。根據式(1),複合流動的複位勢為:
(2)
由此得流函數的方程為。顯然零流線由曲線y=0和x2+y2=m/(2πV∞)組成。前者是Ox軸,後者是半徑為 的圓周。以半徑相同的圓柱代替此圓,流動不受絲毫影響。由此可見,均勻流和偶極子流的疊加在圓外確實是繞圓柱的流動。將m通過a和V∞表出,式(2)可改寫為:
的圓周。以半徑相同的圓柱代替此圓,流動不受絲毫影響。由此可見,均勻流和偶極子流的疊加在圓外確實是繞圓柱的流動。將m通過a和V∞表出,式(2)可改寫為:
奇點分佈法
奇點分佈法
這就是圓柱繞流問題的複位勢。
薄翼繞流問題 用它說明如何應用奇點分佈法解正問題。具有較小的相對厚度和相對彎度的翼型稱為薄翼型。在無粘性不可壓縮無旋運動範圍內,小攻角薄翼型繞流問題的最主要的特性就是翼型對來流的擾動是小擾動。因此翼型上的邊界條件可以線性化。
薄翼型繞流問題可分解為①零攻角繞對稱翼型的流動和②小攻角繞彎弧的流動(圖2)。對稱翼型的厚度分佈和彎弧的彎度分佈分別取薄翼型的對應值。由於第一個問題對舉力和力矩沒有貢獻,所以對氣動力計算來說只須解第二個問題。運用奇點分佈法在翼弦AB上放置強度為γ(x)的渦旋分佈,令其滿足繞流條件,得確定渦旋分佈的積分方程:
奇點分佈法
式中l為弦長;α為攻角;F嚧為翼型中線的y坐標。令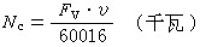 然後將γ(θ)展成θ的三角函數:
然後將γ(θ)展成θ的三角函數:
奇點分佈法
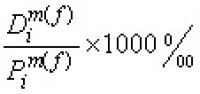
奇點分佈法
式中這一項是考慮到θ=0處有奇性而加的;A0,…,An為待定係數。將式(5)代入式(4)可得:
奇點分佈法
奇點分佈法
由此可計算舉力係數CL和力矩係數CM:
奇點分佈法
式中
奇點分佈法
近年來,由於計算機的發展,奇點分佈法已成為計算流體力學中的一個重要方法──有限基本解法。