高斯光束

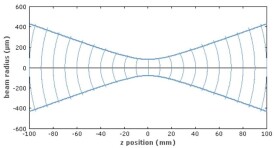
我們常常會收到客戶關於光斑大小的查詢，其實問的就是光斑的束腰直徑或束腰半徑。束腰，是指高斯光絕對平行傳輸的地方。半徑，是指在高斯光的橫截面考察，以最大振幅處為原點，振幅下降到原點處的0.36788倍，也就是1/e倍的地方，由於高斯光關於原點對稱，所以1/e的地方形成一個圓，該圓的半徑，就是光斑在此橫截面的半徑；如果取束腰處的橫截面來考察，此時的半徑，即是束腰半徑。沿著光斑前進，各處的半徑的包絡線是一個雙曲面，該雙曲面有漸近線。高斯光束的傳輸特性，是在遠處沿傳播方向成特定角度擴散，該角度即是光束的遠場發散角，也就是一對漸近線的夾角，它與波長成正比，與其束腰半徑成反比，計算式是：2*波長/（3.1415926*束腰半徑），故而，束腰半徑越小，光斑發散越快；束腰半徑越大，光斑發散越慢。光斑描述如下圖：

我們用感光片可以看到，在近距離時，准直器發出的光在一定範圍內近似成平行光，距離稍遠，光斑逐漸發散，亮點變弱變大；可是從光纖出來的光，很快就發散；這是因為，准直器的光斑直徑大約有400微米，而光纖的光斑直徑不到10微米。同時，對於准直器最大工作距離的定義，往往可理解為該准直器輸出光斑的共焦參數，該參數與光斑束腰半徑平方成正比，與波長成反比，計算式是：3.1415926*束腰半徑*束腰半徑/波長。所以要做成長工作距離（意味著在更長的傳輸距離里高斯光束仍近似成平行光）的准直器，必然要把光斑做大，透鏡相應要加長加粗。

我們對於准直系統的計算，理論根據就是高斯光束的傳輸特性計算式。對於線度遠大於輸入光斑的透鏡來講，該輸入光可視為點光源，其遠場發散角就是該點光源的“邊沿線”夾角；於是我們可根據透鏡的具體參數，簡單的用幾何光學的方法計算該准直系統的光斑大小和最大工作距離。

而從高斯函數，我們可以計算當通光孔徑多大時，光能的損失是多少。並不是通光區直徑等於或略大於光斑直徑時，光能就可以完全通過，事實上，此時的損耗高達0.6dB。簡單的估計，是讓通光直徑是光斑的2倍或以上。

振幅分佈特性

由高斯光束的表達式可以得到：

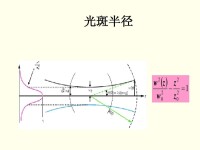
在z截面上，其振幅按照高斯函數規律變化，如圖1所示。將在光束截面內，振幅下降到最大值的1/e時，離光軸的距離定義為該處的光斑半徑。

由w（z）的定義可以得到：

即光束半徑隨傳輸距離的變化規律為雙曲線，在z=0時有最小值，這個位置被稱為高斯光束的束腰位置。

等相位面特性

從高斯光束解的相位部分可以得到傳輸過程中的總相移為：

將上式同標準球面波的總相移表達式比較：

可以得出結論，在近軸條件下高斯光束的等相位面是以R(z)為半徑的球面，球面的球心位置隨著光束的傳播不斷變化，由R(z)的表達式可知：

z=0時，，此時的等相位面是平面；

時，。此時等相位面也是平面。

時，。此時的等相位面半徑最小。

高斯光束的瑞利長度

–當光束從束腰傳播到處時，光束半徑，即光斑面積增大為最小值的兩倍，這個範圍稱為瑞利範圍，從束腰到該處的長度稱為高斯光束的瑞利長度，通常記作f。

在實際應用中，一般認為基模高斯光束在瑞利長度範圍內是近似平行的，因此也把瑞利距離長度稱為準直距離。從瑞利長度表達式可以得出結論，高斯光束的束腰半徑越大，其准直距離越長，准直性越好。

高斯光束的遠場發散角

–從高斯光束的等相位面半徑以及光束半徑的分佈規律可以知道，在瑞利長度之外，高斯光束迅速發散，定義當時高斯光束振幅減小到最大值1/e處與z軸夾角為高斯光束的遠場發散角（半形）：

包含在全遠場發散角內的光束功率占高斯光束總功率的86.5%。

高斯光束在軸線附近可以看成一種非均勻高斯球面波，在傳播過程中曲率中心不斷改變，其振幅在橫截面內為一高斯分佈，強度集中在軸線及其附近，且等相位面保持球面。