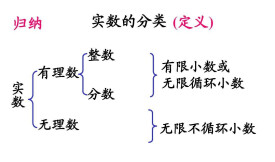
實數集

包含所有有理數和無理數的集合

實數集通俗地認為，通常包含所有有理數和無理數的集合就是實數集，通常用大寫字母R表示。18世紀，微積分學在實數的基礎上發展起來。但當時的實數集並沒有精確的定義。直到1871年，德國數學家康托爾第一次提出了實數的嚴格定義。任何一個非空有上界的集合（包含於R）必有上確界。

目錄

1簡介 2加法定理 3乘法定理

4序公理 5完備公理

簡介

通俗地認為，通常包含所有有理數和無理數的集合就是實數集，通常用大寫字母 R表示。

定義是由四組公理為基礎的：

加法定理

1.1.對於任意屬於集合 R的元素 a、 b，可以定義它們的加法 a+ b，且 a+ b屬於 R；

1.2.加法有恆元0，且 a+0=0+ a= a（從而存在相反數）；

1.3.加法有交換律， a+ b= b+ a；

1.4.加法有結合律，( a+ b)+ c= a+( b+ c)。

乘法定理

2.1對於任意屬於集合 R的元素 a、 b，可以定義它們的乘法 a· b，且 a· b屬於 R；

2.2乘法有恆元1，且 a·1=1· a= a（從而除0外存在倒數）；

2.3乘法有交換律， a· b= b· a；

2.4乘法有結合律，( a· b)· c= a·( b· c)；

2.5乘法對加法有分配率，即 a·( b+ c)=( b+ c)· a= a· b+ a· c。

序公理

3.1∀ x、 y∈ R， x< y、 x= y、 x> y中有且只有一個成立；

3.2若 x< y，∀ z∈ R， x+ z< y+ z；

3.3若 x< y， z>0，則 x· z< y· z；

3.4傳遞性：若 x< y， y< z，則 x< z。

完備公理

(1)任何一個非空有上界的集合（包含於 R）必有上確界。

(2)設 A、 B是兩個包含於 R的集合，且對任何 x屬於 A， y屬於 B，都有 x< y，那麼必存在 c屬於 R，使得對任何 x 屬於 A， y屬於 B，都有 x< c< y。

符合以上四組公理的任何一個集合都叫做實數集，實數集的元素稱為實數。

目錄