描述函數法

描述函數法是P.J.Daniel在1940年首先提出的，主要用來分析在沒有輸入信號作用時，一類非線性系統的穩定性和自振問題。

描述函數法是從頻率域的角度研究非線性控制系統的穩定性的一種等效線性化方法。在蘇聯文獻中，常把這種方法稱為諧波平衡法。這種方法部不受系統階次的影響，但有一定的近似性。另外，描述函數法只能用於研究系統的頻率響應特性，不能給出時間響應的確切信息。

定義：非線性環節穩態正弦響應中的基波分量與輸入正弦信號的複數比（幅值比，相角差）。

1描述函數 2用途 3控制系統

4準確度

描述函數

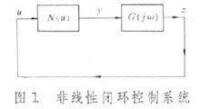
對於一個特性不隨時間變化的非線性元件，輸入是正弦變化並不保證輸出也是正弦變化，但可保證輸出必然是一個周期函數，而且其周期與輸入信號的周期相同。將輸入正弦函數表示為,同時把輸出周期函數y(t)展開成傅里葉級數則非線性元件的描述函數規定為，由輸出的一次諧波分量對輸入正弦函數的振幅之比為模和它們的相位之差為相角組成的一個複函數，其表達式為

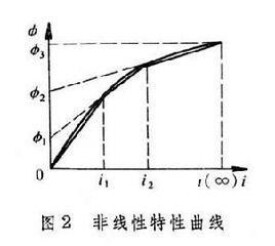
式中X是正弦輸入的振幅,是輸出的一次諧波分量的振幅,是輸出的一次諧波分量與正弦輸入的相位差。因此，一個非線性元件就可採用由描述函數表徵的一個線性元件來等效。這種等效的近似性實質上就是，在使非線性元件與其等效線性元件的輸出偏差均方值為極小意義下的最優逼近。描述函數 N與輸入正弦函數的角頻率ω無關，為輸入正弦函數振幅X的一個複函數。上表列出一些典型的非線性特性的描述函數。

用途

描述函數法

描述函數的一個主要用途是分析非線性控制系統的穩定性，特別是預測系統的自激振蕩（周期運動）。對於一類由線性部件和非線性部件構成的閉環控制系統(圖1)，假定其線性部分為最小相位系統並採用頻率響應表示它的特性，而用描述函數N表示系統中非線性特性的近似等效特性。那麼在同一個複數平面上作出當由0變化到的軌跡和當X由0變化到的軌跡后，就可從這兩個軌跡的相互分佈關係得到判斷此類閉環控制系統的穩定性的一些判據。

穩定和不穩定判據

如果軌跡沒有被軌跡所包圍，則閉環控制系統是穩定的。而當軌跡被軌跡所包圍時，閉環控制系統是不穩定的。在前一情況下，系統不會出現自激振蕩；在後一情況下，系統輸出將增加到安全裝置所限定的極限值。

自激振蕩判據

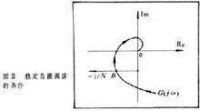
如果軌跡和軌跡相交，則閉環系統的輸出可能出現自激振蕩。這種自激振蕩一般不是正弦的，其角頻率值和振幅值分別為交點處軌跡上的Ω值和軌跡上的X 值。但是，並非所有交點都能構成穩定自激振蕩。只有軌跡的進行方向是由的包圍區過渡到非包圍區的那些交點（如圖2的B點）才能構成穩定自激振蕩。

控制系統

描述函數法對於非線性控制系統的綜合，也提供了方便的工具。通過引入適當的校正裝置可以改變系統線性部分頻率響應軌跡的形狀，從而使閉環控制系統中不出現自激振蕩並確保較好的過渡過程性能。

準確度

描述函數法

描述函數法在分析非線性控制系統中的有效性和準確度，主要取決於非線性元件輸出周期函數中的高次諧波分量在通過線性部分后被衰減的程度。高階線性系統通常具有較好的低通濾波特性，因此用這個方法分析非線性系統時，線性部分為高階時的分析準確度往往比線性部分為低階時好得多。對於判斷自激振蕩，則當軌跡和軌跡接近於垂直相交時，描述函數法的分析準確度較高。

描述函數法