非線性系統
非線性系統
線性系統是狀態變數和輸出變數對於所有可能的輸入變數和初始狀態都滿足疊加原理的系統。一個由線性元部件所組成的系統必是線性系統。但是,相反的命題在某些情況下可能不成立。線性系統的狀態變數(或輸出變數)與輸入變數間的因果關係可用一組線性微分方程或差分方程來描述,這種方程稱為系統的數學模型。非線性系統的分析遠比線性系統為複雜,缺乏能統一處理的有效數學工具。基本分析部分介紹了非線性系統的基本概念和基本分析方法;反饋系統分析部分介紹了輸入-輸出穩定性、無源性和反饋系統的頻域分析;現代分析部分介紹了現代穩定性分析的基本概念、擾動系統的穩定性、擾動理論和平均化以及奇異擾動理論;非線性反饋控制部分介紹了反饋控制的基本概念的反饋線性化,並給出了幾種非線性設計工具,如滑模控制、李雅普諾夫再設計、反步法、基於無源的控制和高增益觀測器等。
線性,指量與量之間按比例、成直線的關係,在空間和時間上代表規則和光滑的運動;而非線性則指不按比例、不成直線的關係,代表不規則的運動和突變。如問:兩個眼睛的視敏度是一個眼睛的幾倍?很容易想到的是兩倍,可實際是6-10倍!這就是非線性:1+1不等於2。激光的生成就是非線性的!當外加電壓較小時,激光器猶如普通電燈,光向四面八方散射;而當外加電壓達到某一定值時,會突然出現一種全新現象:受激原子好像聽到“向右看齊”的命令,發射出相位和方向都一致的單色光,就是激光。非線性的特點是:橫斷各個專業,滲透各個領域,幾乎可以說是:“無處不在時時有。”如:天體運動存在混沌;電、光與聲波的振蕩,會突顯混沌;地磁場在400萬年間,方向突變16次,也是由於混沌。甚至人類自己,原來都是非線性的:與傳統的想法相反,健康人的腦電圖和心臟跳動並不是規則的,而是混沌的,混沌正是生命力的表現,混沌系統對外界的刺激反應,比非混沌系統快。由此可見,非線性就在我們身邊,躲也躲不掉了。
非本質非線性:能夠用小偏差線性化方法進行線性化處理的非線性。
本質是非線性:用小偏差線性化方法不能解決的非線性問題。
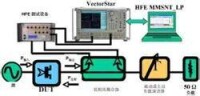
系統中進行精確的非線性測試
定性地說,線性關係只有一種,而非線性關係則千變萬化,不勝枚舉。線性是非線性的特例,它是簡單的比例關係,各部分的貢獻是相互獨立的;而非線性是對這種簡單關係的偏離,各部分之間彼此影響,發生耦合作用,這是產生非線性問題的複雜性和多樣性的根本原因。正因為如此,非線性系統中各種因素的獨立性就喪失了:整體不等於部分之和,疊加原理失效,非線性方程的兩個解之和不再是原方程的解。因此,對於非線性問題只能具體問題具體分析。
線性與非線性現象的區別一般還有以下特徵:
(1)在運動形式上,線性現象一般表現為時空中的平滑運動,並可用性能良好的函數關係表示,而非線性現象則表現為從規則運動向不規則運動的轉化和躍變;
(2)線性系統對外界影響的響應平緩、光滑,而非線性系統中參數的極微小變動,在一些關節點上,可以引起系統運動形式的定性改變。在自然界和人類社會中大量存在的相互作用都是非線性的,線性作用只不過是非線性作用在一定條件下的近似。
第1章、緒論
第2章、二階系統
第3章、基本性質
第4章、李雅普諾夫穩定性
5章、輸入-輸出穩定性
第6章、無源性
第7章、反饋系統的頻域分析
第8章、現代穩定性分析
9章、擾動系統的穩定性
10章、擾動理論和平均化
11章、奇異擾動
12章、反饋控制
13章、反饋線性化
14章、非線性設計工具
附錄A、數學知識複習
附錄B、壓縮映射
附錄C、證明
參考文獻說明
參考文獻
符號表
術語表
作者:(美國)哈里爾(Hassan K.Khalil)譯者:朱義勝、董輝、李作洲等
非線性系統的分析遠比線性系統為複雜,缺乏能統一處理的有效數學工具。在許多工程應用中,由於難以求解出系統的精確輸出過程,通常只限於考慮:①系統是否穩定。②系統是否產生自激振蕩(見非線性振動)及其振幅和頻率的測算方法。③如何限制自激振蕩的幅值以至消除它。例如一個頻率是ω的自激振蕩可被另一個頻率是ω1的振蕩抑制下去,這種非同步抑制現象已被用來抑制某些重型設備的伺服系統中由於齒隙引起的自振蕩。
在工程上還經常遇到一類弱非線性系統,即特性和運動模式與線性系統相差很小的系統。對於這類系統通常以線性系統模型作為一階近似,得出結果后再根據系統的弱非線性加以修正,以便得到較精確的結果。攝動方法是處理這類系統的常用工具。而對於本質非線性系統,則需要用分段線性化法等非線性理論和方法來處理。
現代廣泛應用於工程上的分析方法有基於頻率域分析的描述函數法和波波夫超穩定性等,還有基於時間域分析的相平面法和李雅普諾夫穩定性理論等。這些方法分別在一定的假設條件下,能提供關於系統穩定性或過渡過程的信息。而計算機技術的迅速發展為分析和設計複雜的非線性系統提供了有利的條件。
在某些工程問題中,非線性特性還常被用來改善控制系統的品質。例如將死區特性環節和微分環節同時加到某個二階系統的反饋迴路中去,就可以使系統的控制既快速又平穩。又如,可以利用繼電特性來實現最速控制系統。
非線性控制系統在許多領域都具有廣泛的應用。除了一般工程系統外,在機器人、生態系統和經濟系統的控制中也具有重要意義。
