衍射

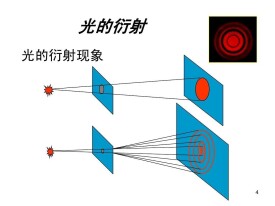
光在傳播路徑中，遇到不透明或透明的障礙物或者小孔（窄縫），繞過障礙物，產生偏離直線傳播的現象稱為光的衍射。衍射時產生的明暗條紋或光環，叫衍射圖樣。

定義：光波遇到障礙物以後會或多或少地偏離幾何光學傳播定律的現象。

包括：單縫衍射、圓孔衍射、圓板衍射及泊松亮斑。

產生衍射的條件是：由於光的波長很短，只有十分之幾微米，通常物體都比它大得多，但是當光射向一個針孔、一條狹縫、一根細絲時，可以清楚地看到光的衍射。用單色光照射時效果好一些，如果用複色光，則看到的衍射圖案是彩色的。

任何障礙物都可以使光發生衍射現象，但發生明顯衍射現象的條件是“苛刻”的。

當障礙物的尺寸遠大於光波的波長時，光可看成沿直線傳播。注意，光的直線傳播只是一種近似的規律，當光的波長比孔或障礙物小得多時，光可看成沿直線傳播；在孔或障礙物可以跟波長相比，甚至比波長還要小時，衍射就十分明顯。由於可見光波長範圍為4×10∧-7m至7.7×10∧-7m之間，所以日常生活中很少見到明顯的光的衍射現象。

惠更斯提出，媒質上波陣面上的各點，都可以看成是發射子波的波源，其後任意時刻這些子波的波跡，就是該時刻新的波陣面。惠更斯－菲涅爾原理能定性地描述衍射現象中光的傳播問題。菲涅爾充實了惠更斯原理，他提出波前上每個面元都可視為子波的波源，在空間某點P的振動是所有這些子波在該點產生的相干振動的疊加，稱為惠更斯－菲涅爾原理。

指的是光源-衍射屏、衍射屏-接受屏之間的距離均為有限遠，或其中之一為有限遠的場合，或者說，球面波照明時在有限遠處接收的是菲涅爾衍射場。例如：圓孔衍射、圓屏衍射菲涅爾衍射、泊松亮斑。

指的是衍射屏與兩者的距離均是無限遠的場合，或者說，平面波照明時在無窮遠處接收的是夫琅禾費衍射場。概略的看，菲涅爾衍射是近場衍射，而夫琅禾費衍射是遠場衍射。不過，在成像衍射系統中，與照明用的點光源相共軛的像面上的衍射場也是夫琅禾費衍射場，此時，衍射屏與點光源或接收屏之距離在現實空間看，都是很近的。

從理論上看，夫琅禾費衍射顯然是菲涅爾衍射的一種特殊情形，而實際上卻更為人們所重視，這是因為夫琅禾費衍射場的理論計算較為容易、應用價值又很大，而實驗上又不難實現。尤其是，在現代變換光學中傅里葉光學的興起，賦予經典夫琅禾費衍射以新的現代光學的意義——傅里葉光學是以夫琅禾費衍射衍射為枝杈生長起來的。

例如：單縫夫琅和費衍射、矩孔和三角孔夫琅禾費衍射、圓孔夫琅禾費衍射。

①狹縫衍射

讓激光發出的單色光照射到狹縫上，當狹縫由很寬逐漸減小，在光屏上出現的現象怎樣？

當狹縫很寬時，縫的寬度遠遠大於光的波長，衍射現象極不明顯，光沿直線傳播，在屏上產生一條跟縫寬度相當的亮線；但當縫的寬度調到很窄，可以跟光波相比擬時，光通過縫后就明顯偏離了直線傳播方向，照射到屏上相當寬的地方，並且出現了明暗相間的衍射條紋，狹縫越小，衍射範圍越大，衍射條紋越寬。但亮度越來越暗。

試驗：可以用遊標卡尺調整到肉眼可辨認的最小距離，再通過此縫看光源

②小孔衍射

當孔半徑較大時，光沿直線傳播，在屏上得到一個按直線傳播計算出來一樣大小的亮光圓斑；減小孔的半徑，屏上將出現按直線傳播計算出來的倒立的光源的像，即小孔成像；繼續減小孔的半徑，屏上將出現明暗相間的圓形衍射光環。

光的衍射效應最早是由弗朗西斯科·格里馬第（Francesco Grimaldi）於1665年發現並加以描述，他也是“衍射”一詞的創始人。這個詞源於拉丁語辭彙diffringere，意為“成為碎片”，即波原來的傳播方向被“打碎”、彎散至不同的方向。格里馬第觀察到的現象直到1665年才被發表，這時他已經去世。他提出

“光不僅會沿直線傳播、折射和反射，還能夠以第四種方式傳播，即通過衍射的形式傳播。”（"Propositio I. Lumen propagatur seu diffunditur non solum directe, refracte, ac reflexe, sed etiam alio quodam quarto modo, diffracte."）

英國科學家艾薩克·牛頓對這些現象進行了研究，他認為光線發生了彎曲，並認為光是由粒子構成。在19世紀以前，由於牛頓在學界的權威，光的粒子說在很長一段時間佔有主流位置。這樣的情況直到19世紀幾項理論和實驗結果的發表，才得以改變。1803年，托馬斯·楊進行了一項非常著名的實驗，這項實驗展示了兩條緊密相鄰的狹縫造成的干涉現象，後人稱之為“雙縫實驗”。在這個實驗中，一束光照射到具有緊挨的兩條狹縫的遮光擋板上，當光穿過狹縫並照射到擋板後面的觀察屏上，可以產生明暗相間的條紋。他把這歸因於光束通過兩條狹縫后衍射產生的干涉現象，並進一步推測光一定具有波動的性質。奧古斯丁·菲涅耳則對衍射做了更多權威的計算研究，他的結果分別於1815年和1818年被發表，他提到

“這樣，我就展示了人們能夠通過何種方式來構想光以球面波連續不斷地傳播出去……”（ "J'ai donc montré de quelle façon l'on peut concevoir que la lumière s'étend successivement par des ondes sphériques, ..."）

法國科學院曾經舉辦了一個關於衍射問題的有獎辯論會，菲涅耳贏得了這次辯論。作為反對光波動學說的其中一位，西莫恩·德尼·泊松提出，如果菲涅耳聲稱的結論是正確的，那麼當光射向一個球的時候，將會在球後面陰影區域的中心找到亮斑。結果，評審委員會安排了上述實驗，並發現了位於陰影區域中心的亮斑（它後來被稱作泊松光斑）。這個發現極大地支持了菲涅耳的理論。

他的研究為克里斯蒂安·惠更斯發展的光的波動理論提供了很大的支持。他與楊的理論共同反駁了牛頓關於光是粒子的理論。

在對衍射現象的探索過程中，人們也不斷積累了對於衍射光柵的認識。17世紀，蘇格蘭數學家、天文學家詹姆斯·格雷戈里（James Gregory）在鳥的羽毛縫間觀察到了陽光的衍射現象。他是第一個發現衍射光柵原理的科學家。在1673年5月13日他寫給約翰·科林斯（John Colins）的一封信中提到了此發現。；1786年，美國天文學家戴維·里滕豪斯用螺絲和細線第一次人工製成了衍射光柵，細線的密度達到每英寸100線，他用這個裝置成功地看到了陽光的衍射。1821年，約瑟夫·夫琅禾費利用相似的裝置（每厘米127線）證明了托馬斯·楊關於衍射的公式（參見段落下方），並對衍射進行了許多重要研究。1867年，劉易斯·盧瑟福（Lewis Morris Rutherfurd）採用水輪機作為動力進行刻線、製作光柵。後來的亨利·奧古斯塔斯·羅蘭 改良了光柵的刻劃技術，並在1882年發明了在凹形球面鏡上進行刻劃的凹面光柵。其後的羅伯特·伍德（Robert William Wood）改進了光柵的刻劃形狀，從而提高了光柵的衍射效率。近代的阿爾伯特·邁克耳孫提出利用干涉伺服系統控制光柵的刻劃過程，於1948年實現了這一想法。20世紀下半葉，由於激光、光刻膠等新技術的出現，光柵製造技術取得很大的進步，製造成本顯著降低，製造周期也得以縮短。

如果採用單色平行光，則衍射后將產生干涉結果。相干波在空間某處相遇后，因位相不同，相互之間產生干涉作用，引起相互加強或減弱的物理現象。衍射的結果是產生明暗相間的衍射花紋，代表著衍射方向（角度）和強度。根據衍射花紋可以反過來推測光源和光柵的情況。為了

使光能產生明顯的偏向，必須使“光柵間隔”具有與光的波長相同的數量級。用於可見光譜的光柵每毫米要刻有約500條線。

1912年，勞厄想到，如果晶體中的原子排列是有規則的，那麼晶體可以當作是X射線的三維衍射光柵。X射線波長的數量級是10^-8cm,這與固體中的原子間距大致相同。果然試驗取得了成功，這就是最早的X射線衍射。顯然，在X射線一定的情況下，根據衍射的花樣可以分析晶體的性質。但為此必須事先建立X射線衍射的方向和強度與晶體結構之間的對應關係。

應用射線概念分析電磁波衍射特性的漸近理論，簡稱 GTD。幾何理論是單色波場方程的解在頻率趨於無限時的極限，因而也是適合於高頻情形的漸近解，而這種理論的基本思想是把均勻平面波在無限平界面上的反射和折射、在半無限楔形導體邊緣上的衍射和沿圓柱導體表面的爬行波嚴格解的漸近式，應用於從點源發出的球面波或線源發出的柱面波在圓滑界面上的反射和折射、在弧形導體刃口上的衍射和沿導體凸表面的爬行，並把它作為問題的0階段近解。

衍射的幾何理論

② 反射係數、衍射係數和爬行線的衰減係數採用無限直刃和無限長圓柱上嚴格解的漸近結果。

③ 投射波、反射波和衍射波的場強各與其主曲率半徑的幾何平均數成反比，而確定反射波和衍射波曲率矩陣的原則是相位匹配。所謂相位匹配，如圖3，設A是衍射點，A┡是其鄰點，則，A、A┡兩點所在的衍射波面的相位差與 A、A┡兩點所在的投射波面的相位差應當相同。

衍射的幾何理論最早是由J.B.凱勒於1957年提出來的，後來經許多人的工作而日趨完善，在處理很多異形物體的散射問題以及用數值計算解散射和衍射問題中得到應用。但是，因為嚴格解的漸近式在陰影區與照明區的過渡區域不能成立，所以在這個區域，GTD 不能應用，為了彌補這一缺陷，J.波斯馬等人後來提出一致漸近理論 (UAT)。這個理論的基本思想是，給投射波乘以人為因子，使這因子在照明區內近於1而在陰影區內近於0,在過渡區內則隨著場點趨近於照明區邊界而無限增大。將這乘了因子的投射波與衍射波的漸近式相加能一致連續，這種理論也得到了廣泛的應用。但是，它的基礎僅僅是一個估值(ansatz),而且在刃口以及其他焦散線附近，它和 GTD同樣不能應用。然而射線理論有很多優點，人們仍在探索改進的途徑。