多重分形
多重分形
多重分形(multifractal)一種分為多個區域的複雜分形結構。為了對分形的複雜性和不均勻性進行更細緻地刻畫,需引進它的概率分佈函數及其各階矩的計算,由此構成了分形維數的一個連續譜,稱之為多重分形或多標度分形。
目錄
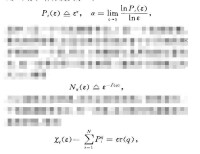
多重分形
r(y)常稱為質量指數。再定義加權后的廣義分形維數D。為
這一系列公式給出了多重分形理論的基本核心。利用多重分形,可把一個複雜的分形分成許多具有不同奇異程度的小區域來研究,從而能分層次地來了解分形的內部精細結構.
多重分形(multifractal)一種分為多個區域的複雜分形結構。為了對分形的複雜性和不均勻性進行更細緻地刻畫,需引進它的概率分佈函數及其各階矩的計算,由此構成了分形維數的一個連續譜,稱之為多重分形或多標度分形。
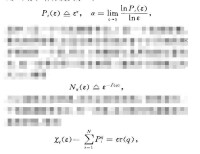
目錄