集值映射
集值映射
集值映射亦稱多值映射,映射概念的推廣。設X和Y是兩個集合,記2Y=A|A⊂Y,稱之為Y的冪集,從X到Y的一個集值映射指的是從X到2Y的一個單值映射F:X→2Y,對於A⊂X,F(A)=∪F(x)|x∈A稱為A在F下的像,graph(F)=(x,y)∈X×Y|x∈X,y∈F(x)稱為F的圖象,任意給定Γ⊂X×Y,則由F(x)=y∈Y|(x,y)∈Γ(ᗄx∈X)可惟一確定集值映射F:X→2Y,使得graph(F)=Γ,由F(y)=x∈X|(x,y)∈graph(F)(ᗄy∈Y)定義的集值映射F:Y→2稱為F的逆映射。設有F:X→2Y,dom(F)=x∈X|F(x)≠∅稱為F的有效域,若ᗄx∈X有F(x)≠∅,則稱F具非空值,這時dom(F)=X,當Y是拓撲空間或賦范線性空間時,若ᗄx∈X,F(x)為閉集(相應地,緊集、凸集、有界集等),則稱F具閉值(相應地,具緊值、凸值、有界值等)。
對於兩個集合,如果按照一個對應關係(規則),使得對於 中的每一元素,都有 中的一個(幾個)確定的元素 與之對應,那麼我們把這個對應關係叫做集合 到集合 的單值(多值)映射,多值映射也稱“集值映射”。通常用 …等符號來代表映射,當 表示一個由集合 到集合 的映射,那麼記,或,對任意,對於任意集合,我們把集合 叫做的象,而對任何集合,我們把集合 叫做 的原象(逆象)。
定義1
對任意的 和任意 成立,那麼我們稱函數 為 上的凹函數。當不等式是嚴格不等式時,我們叫 為嚴格凹函數。
類似可定義凸函數。凹函數圖像如圖1。
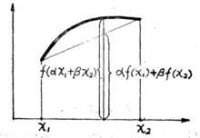
圖1
定義2
對多值映射 序列,如果當 且 時有,那麼,我們說映射 是上半連續的。
當 為單值映射時,以上就是它的連續性定義。
定義3
若從 能夠推出存在 使得 則稱映射 為下半連續。
由定義得知,要證明映射的下半連續性,就要找出滿足定義條件的序列 來。
關於多值映射的線性組合,我們有如下定義。
定義4
假定有幾個映射 是上半連續的,是凸且有界閉的集合,那麼映射
叫做映射 的線性組合,並用記號。
假定集合 是凸,有界閉集,定必在 上的連續函數 關於 是凹的,那麼映射
是上半連續的,且集合是非空凸、閉集。
假定集合X與Y是凸、有界閉集,函數定義在 上,且對x與y分別是連續的,對y是凸的,如果存在,使得對所有 滿足。那麼映射 既是上半連續又是下半連續,並且集合是非空,凸且閉的。
假定連續函數定義在上,其中是凸,有界閉集,對y是凹的,並且多值映射是上半且下半連續的,集非空,對任意是凸的。那麼映射
是上半連續的,集合是非空,凸且有界閉的集合。
關於多值映射的線性組合,有如下結論。
上半連續映射的線性組合也是上半連續的。
下述的日本學者卡庫坦的多值映射不動點定理,在經濟數學中佔有重要地位。
假定是凸且有界閉的中的子集,映射是上半連續的,集合是非空凸集,那麼存在,使。