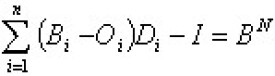多值映射
多值映射
多值映射(multivalued mapping )亦稱集值映射(setvalued mapping),是映射概念的推廣,屬於拓撲學的一個基本概念。設X和Y是兩個集合,記2={A|A⊂Y},稱之為Y的冪集,從X到Y的一個集值映射指的是從X到2的一個單值映射F:X→2。對於A⊂X,F(A)=∪{F(x)|x∈A}稱為A在F下的像,graph(F)={(x,y)∈X×Y|x∈X,y∈F(x)}稱為F的圖象。任意給定Γ⊂X×Y,則由F(x)={y∈Y|(x,y)∈Γ}(ᗄx∈X)可惟一確定集值映射F:X→2,使得graph(F)=Γ。由F(y)={x∈X|(x,y)∈graph(F)}(ᗄy∈Y)定義的集值映射F:Y→2稱為F的逆映射。設有F:X→2,dom(F)={x∈X|F(x)≠∅}稱為F的有效域,若ᗄx∈X有F(x)≠∅,則稱F具非空值,這時dom(F)=X,當Y是拓撲空間或賦范線性空間時,若ᗄx∈X,F(x)為閉集(相應地,緊集,凸集,有界集等),則稱F具閉值(相應地,具緊值,凸值,有界值等)
目錄
從集X到集Y的多值映射是一個對應規律F,按照這個規律,對於X的每個元素x,都能相應地得到Y的一個非空子集F(x),稱為x對於F的像。對於任何,集稱為集X對於F的像;按照或而說F把X映入或映成Y。特別是,如果每個元素的像集都只含有一個元素,那就是一個單值映射。空間與(單值)映射是拓撲學中兩個最原始的基本概念,拓撲學的基本問題──空間的拓撲分類問題,是基於同胚的概念提出來的。而同胚是單值映射,所以單值映射在拓撲學中的地位,顯然遠比多值映射的地位重要得多。實際上,提出多值映射的概念,出發點不是單純為了推廣,而是著眼於它對其他數學領域的應用。多值映射總是可以化成單值映射來考慮的,即是,如果用到Y的多值映射定義它的逆像為,所以對於任何的連續性,的拓撲結構 τY)給出的,通常有下面三種:對於任何,定義,於是以為子基產生的拓撲結構稱為維托利斯拓撲,而以或為子基產生的拓撲結構則分別稱為上半連續拓撲和下半連續拓撲。在這些拓撲結構下, (作為單值映射)的連續性分別稱為連續、上半連續或下半連續,即是,稱為上半連續的,如果F稱為下半連續的,如果F稱為連續的,如果它既是上半連續又是下半連續的;這裡稱為集U的上逆像,而稱為集U的下逆像。子集空間的拓撲結構對於由此展開的多值映射理論至關緊要,因此,對於子集空間拓撲結構的研究已經成為點集拓撲學中一個有趣的課題。此外,對於多值映射還可以提出一個連續選擇的問題:在什麼條件下存在單值連續映射,使得?如果F具有連續選擇,那麼與F 有關的應用問題幾乎都可以歸結為單值映射的相應問題。
多值映射的一般理論自然是單值映射相應理論的推廣,但前者顯然不如後者那麼豐富多彩。多值映射理論的重要性在於它對其他數學分支的應用,特別值得一提的,是多值映射的不動點理論對博弈論的完美應用。稱為的不動點,如果。角谷靜夫於1941年首先把關於單值映射的布勞威爾不動點定理推廣到多值映射,下面是一個等價形式:
角谷不動點定理 假設是非空有界閉凸集,是上半連續多值映射,使得對每個都是K的非空閉凸集,於是F有不動點。
命,於是是非空有界閉凸集。考慮雙線性函數
為實矩陣。對於任何,命可以證明,是非空閉凸集,上半連續,所以據角谷定理知,存在,使 ,即
從而
由於相反的不等式是自然成立的,這就證明了矩陣博弈的基本定理:存在∈Δ,使得
現在角谷定理已經得到很大的推廣,在博弈論、泛函分析等分支都有廣泛而重要的應用。
參考書目
E.Michael,Topologies on Spaces of Subsets,Tran. Amer.Math. Soc., Vol.71, pp.152~182,1951.
E.Michael, A Survey of Continuous Selections,Lecture Notes in Math.,Vol.171, Springer-Verlag, Berlin, 1970.
C.Berge,Topological Spaces, Oliver and Boyd, Edinbergh and London, 1963.
C. Berge,Théorie Générale des Jeux ╜ n Personnes,Gauthier-Villars, Paris, 1957.