相似變換
幾何術語之一
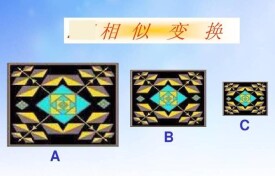
圖形的相似變換是指由一個圖形到另一個圖形,在改變的過程中保持形狀不變(大小方向和位置可變)的圖形。
相似變換簡稱相似。歐幾里得幾何中的一類變換。任意兩點P、Q與其像點P'、Q'滿足|P'Q'|/|PQ|=k(k為非零常數)的變化。常數k稱為相似比(similarity ratio)。當k=1時,即為合同變換。相似變換可以表示成一個合同變換和一個位似變換的乘積。相似變換把圖形變成它和相似的圖形。相似變換保持兩直線所成角大小不變,並且不改變圖形形狀只改變其大小。
平面內有兩種相似變換:
1、真正的相似變換(正相似變換);
2、鏡像相似變換(負相似變換)。
真正相似變換把一個圖形變換成與它真正相似(正相似)的圖形,即使得兩個相似圖形的每對對應三角形有同一的方向,每對對應角有同一方向。
鏡像相似變換把一個圖形換成與它鏡像相似的(負相似)圖形。即使得兩個相似圖形的每對對應三角形有相反的方向,每對對應角有相反的方向。
相似變換的逆變換也是相似變換,兩個相似變換的乘積仍是相似變換,所有的相似變換的全體構成一個群,稱為相似變化群(similarity transformation group)。
圖形相似變換的性質
圖形的相似變換不改變圖形中每一個角的大小;
圖形相似變換后對應線段都擴大(或縮小)相同的倍數,這個數叫相似比。
相似變換面積
經相似變換的像與原圖的面積等於相似比的平方。
相似變換的分解
任何相似變換可以分解為放縮,平移,旋轉和翻轉變換的複合。相似變換是仿射變換的一種特殊情況,也就是在仿射變換中去除錯位變換這個因子后的結果。
定義
任何方陣通過復相似變換可以變化到一種標準的分塊對角陣形式,其中每個分塊的對角線元相同,為矩陣M的特徵值,除此以外,僅對角線上面的副對角線元素為1,其餘都為0。或者說存在復可逆矩陣P,使得
P^-1MP=ding{R1,R2,…,Rt}
其中Ri形如λI+N,其中I為單位矩陣,N為和I同階的僅對角線上面次對角線元素為1其餘元素都是0的矩陣,即形如:
| 0 1 0 … 0 0 |
| 0 0 1 … 0 0 |
|… … … … |
| 0 0 0 … 1 0 |
| 0 0 0 … 0 1 |
| 0 0 0 … 0 0 |
當然特別的,如果Ri是一階的,I就是數字1,N是數字0。