阿羅悖論
阿羅悖論
阿羅悖論是指經濟學中,經常提出一些目標體系。按照實際經濟運行是貼近於它及貼近程度,還是背離了它及背離幅度,來判斷經濟運行的好壞。
阿羅悖論(Arrow Paradox)又稱作阿羅不可能定理(Arrow's impossible theorem),是由1972年諾貝爾經濟學獎的獲得者之一肯尼斯·約瑟夫·阿羅(Kenneth J.Arrow)首先陳述和證明的。如下:

阿羅悖論
經濟學中,經常提出一些目標體系。按照實際經濟運行是貼近於它及貼近程度,還是背離了它及背離幅度,來判斷經濟運行的好壞。最一般地,人們提出一個經濟體制應該具備兩大社會目標。
a. 最大的選擇自由。選擇自由主要是指:個人有權自由選擇職業,自由提供生產要素,自由經營企業,自由的買賣產品,自由安排工作和休閑時間等等。
徠b.最高的經濟效率。在既定的生產資源、生產技術等,通過資源的最優配置和利用,達到最高的產品生產效率;然後通過各種途徑,即:自願交換或者收入轉移,讓既得產品於消費時,提供給人以儘可能多的效用滿足,從而獲得最高的產品消費效率。阿羅悖論的起源,應該包含兩個方面。一個是歷史的起源,另一個是機制的起源。
1. 阿羅定理的歷史起源
談及阿羅悖論的歷史起源,則應該從福利經濟學說起。福利經濟學從提出至今,大致走過了三個里程碑。
第一個里程碑是庇古的經濟福利學,稱為舊福利經濟學。它包含著兩個基本命題:第一,國民生產純產值越大,社會經濟福利就越大;第二,國民收入分配越是平等,社會經濟福利就越大。
第二個里程碑是以帕累托最優狀態命名的新福利經濟學。他們提出福利最大狀態實質是效率最大狀態,表述如下:在經濟運行時,如對現狀進行的改變,使得至少有一個人的福利增進了,這種改變就有利;如果使得至少一個人的福利減少了,這種改變就不利;但是,如果使得一個人的福利增進的同時,而使得另一個人的福利減少,就不能說這種改變一定有利或者不利。然而就是在此時,卻達到了帕累托最優狀態。經濟學家們通過嚴格的推理證明:在完全競爭的條件下,如果消費者追求最大效用滿足,生產者追求最多利潤獲得,生產要素所有者追求最大收入,加上沒有經濟外部效應,就一定能夠達到社會福利最大的帕累托最優狀態。
第三個里程碑,則是以伯格森、薩繆爾森為代表的社會福利函數派。社會福利函數派認為,因為不同的收入分配會對消費和生產發生不同的影響,因此福利經濟學不應該排除收入分配問題。帕累托的最優狀態只解決了經濟效率問題,沒有解決合理分配問題。如果一個人獨霸全世界的山河土地,仍會存在著相應的一個帕累托最優狀態。他們認為,經濟效率僅是社會福利最大的必要條件,而合理分配產品收入是社會福利最大的充分條件,只有同時解決效率和公平的問題,才能達到社會福利的唯一最優狀態。
為此,他們殫盡心力地尋找社會福利函數。他們以政治投票與貨幣投票具有相似特徵出發,提出用政治投票的方式構建社會福利函數。但是,遺憾的是,阿羅卻以嚴格的數理邏輯推導出了投票悖論,以形式化的方式證明了無法以投票的方式產生人人都能接受的唯一社會福利函數。這使得社會福利函數派的公平設想歸於毀滅。
然而,阿羅悖論所說的投票悖論引發的更是一場深刻的經濟理論危機。阿羅悖論從最深邃意義上可以被理解成:個人私自利益與社會整體利益無論如何必然存在矛盾,不能在滿足所有個人私有利益的前提下,邏輯地導出社會整體利益同時也被滿足的結論。
阿羅悖論使多年來福利經濟學的成果毀於一旦。同時,我們還要進一步看到悖論揭示的深刻性。因為,從亞當·斯密開始的“看不見的手”論述,即整個西方經濟學關於市場經濟導致資源配置最優化的概念,是從個人利益被滿足的同時,會自動地導向全社會資源配置的總體優化為前提的。設想,當將政治投票形式換成貨幣投票形式,則問題的嚴重性就凸顯出來。因為,阿羅悖論已經脫離了具體內容,用公理化的形式,證明了從上述的前提到結論是絕對不可能的。這樣一來,西方經濟學的整個大廈基礎都將被傾覆,市場經濟的所有現成結論都被推翻。
推理很深奧,思想很深刻,挑戰很嚴厲,事態很嚴重。然而問題究竟出在何處?問題是,當理論家下意識地理解阿羅悖論時,都把人們的政治投票選擇行為等同於人們的貨幣投票選擇行為。這也包括阿羅本人。他寫道:“投票和市場的方法,是彙集許多不同的個人趣味來做出社會選擇的方式。“"同樣地,市場機制也不能產生一合理的社會選擇。”“任一社會福利函數必定要麼是強加的,要麼就是獨裁性的。“
2. 機制起源
一個經濟社會總存在著它擁有的生產資源,比如土地、資本、勞動等等。擁有這些生產資源,如何進行要素的配置,以使得它們能夠以帕累托描述的方法進行最有效率的生產呢?而對生產獲得到的產品進行消費,又如何能夠達到帕累托最有效率狀態呢?
一般都用兩人、兩種產品、兩種生產要素,以埃奇沃思箱形圖來直觀地說明問題。雖然,埃奇沃思箱形圖僅能清晰地說明2×2×2情形的帕累托最優狀態配置,但是,阿羅—德布魯定理已經全面地證明任意位個人、任意種產品和任意類生產要素的帕累托最優狀態配置。所以,定性地用埃奇沃思箱形圖來說明問題,並不影響結論的準確性。
是一個兩人社會用它擁有兩種生產要素,l數量的勞動和k 數量的資本,生產兩種產品x和y。l數量勞動和k數量資本形成了埃奇沃思箱形圖的兩條邊長,表示生產要素的有限性。這時,可根據社會當時的技術水平,畫出x、y兩種產品的等產量曲線族。
其中從原點o[,x]開始,向右上方度量生產x 產品所使用的兩種生產要素數量,用橫軸l[,x]和豎軸k[,x]標度分別表示,即可得圖中標明的q[,1]、q[,2]、q[,3]、q[,4]這些等產量曲線。類似地從o[,y] 向左下度量生產y產品使用的兩種生產要素數量,就有y產量的等產量曲線。
很明顯,當於圖1的a點處分配勞動和資本來生產x、y兩種產品時,就不是帕累托最優狀態。因為,把勞動與資本的分割點沿著x或y的某一條等產量曲線向右下前進,都可在該種產品生產數量不減的同時,獲得另一種產品生產數量增加。調整的過程一直可以進行到這條曲線與對偶某條曲線相切為止。比如圖1中的b點和c點。b點和c 點處的生產要素使用效率就是最有效率的帕累托境界。因為此時,若要再增加x 產品數量生產,就必然導致y產品數量的減少,反之亦然。
類似b和c這樣的x、y產品等產量線相切點的全體,在埃奇沃思箱形圖內形成了一條新曲線,稱之為生產契約曲線。它從左下角的o[,x] 出發,一直延伸到右上角的o[,y]為止。這條線上的生產要素配置方式都達到了帕累托最有效率配置。
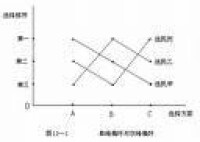
把沿著這條線上行進得到的x產量和y產量同時記錄下來,轉換到一個新的坐標系,即產品數量坐標系中,則可得到如許固定有限的l和k,可達到的x、y最多產量的組合曲線,稱之為生產可能性曲線。
一種生產極大化狀態,對應的就是圖2 中生產可能性曲線上的某一點。如果我們在圖2中取d點,則d 點就是甲乙兩人獲得的最大數量共同產品。那麼,他倆怎樣才能從d點所表示的x、y 產品中獲得最多的效用呢?
可以根據他倆的無差異效用偏好曲線作出。左下角的原點o,是測量甲效用的原點,位於生產可能性曲線上的d點,即右上角的點,是測量乙的原點。兩人分別具有的無差異偏好曲線是i[,甲1]、i[,甲2]和i[,甲3],i[,乙1]、i[,乙2]和i[,乙3]。在圖2中,甲的i[,甲1] 和乙的i[,乙2]相交於e點。e點即表示x、y產品在兩人中的一種分配方式,但是,e點並不是帕累托最優點。因為,沿著任一人的無差異曲線向右下方移動后,都會使得另一人的效用增加。只有當到達g點或者f點時,進一步的移動才會導致另一人的效用減少。觀察g點和f點處,兩人的無差異偏好曲線正恰相切。
當把兩個無差異偏好曲線族的所有兩兩相切點都找出后,就得到了消費時表示的帕累托最優狀態的曲線——連接兩個原點o-d 的交換契約曲線。
沿著交換契約曲線移動的同時,記錄兩人效用大小的變化。如把兩人效用大小的變化轉移到表示甲乙兩人的效用坐標系中,就得到了兩人的總效用變化曲線。
這條曲線顯示的僅僅是圖2生產可能性曲線d點處標示的那種合x、y產量,於甲乙兩人間各種不同分配所形成兩人總效用變化曲線。於是,可知現時的這條總效用變化曲線,是兩人用既定的l和k生產要素,生產特定數量x、y產品組合后,消費所能獲得的極大化表示。
生產可能性曲線上的每一點,都是兩人極大化生產的可能點。而對應每一點的極大化x、y產品,都可以查找到兩人不同分配數量形成的總效用變化曲線。於是可作出無數條總效用變化曲線。由所有總效用變化曲線形成了的最外面的包絡線,就是總效用的可能曲線。曲線參見圖3外沿的虛線。
的總效用可能曲線就是甲乙兩人消去了x、y 產品數量的種種可能變化后,即消去了中間變數,所能夠獲得帕累托最優狀態的情形。這時,他倆既具備著最高的生產效率,也獲得了最大消費福利。
可以把上面所述的總效用可能曲線,理解為飛機的最大飛行半徑,上面的任意一點都是可以著落的機場。然而,僅從上面得到的經濟運行結果,卻還是一個無約束的結果,或者是約束過少的結果。由此人們並無法獲知一個確定的解答案。
這裡缺少了什麼?缺少了分配的介入。自然,人們要追問,經濟運行的分配是否可以自然而然地決定呢?還是可依人們願望加以自行挑選的呢?對於這個設問的回答,馬上就引出了人們的公平觀念以及用政治投票決定經濟選擇的行為思考。

阿羅悖論圖示
這樣的解具有唯一性嗎?答案是:具有唯一性。
因為按分配函數,勞動、資本等等具有邊際遞減傾向的生產要素分配份額,由它們的邊際生產率決定。而如技術進步、風險、壟斷等引起的分配,是由生產出來的產品,除去上述的勞動、資本等要素分配后才決定的。在一組方程式中,由以上各項決定的分配是不可變更的,具有唯一性。
但市場經濟的“自然”運行解,帶有一個最令人們傷透腦筋的副作用,即“馬太”效應。“自然”運行解具有正反饋的過程和結局,它使得人與人之間相比,不但收入,而且生產資料都越來越不平均,產生富者愈富、貧者愈貧的兩極分化結果。
人們對此進行了反思與質問。因為,自然提供給人的生產要素,應該看成是提供給人類的全體,而並非提供給人類的某些人或某部分人。從這點出發,任何個人或部分人利用或者“霸佔”自然提供的生產要素,在分配中佔有不恰當的一份,都是不能令人滿意和接受的。
這就是福利經濟學所看到的問題,並且他們還從中提煉出解決問題的方式:為什麼不能在保持“自然”分配前提下,再追加另外方式,而不全然用自然強加的“自然”性的邊際生產率方式,來進行產品的分配呢?或者通俗地說,用二次分配的方式來進行社會產品的再分配。
從這點出發,他們引出了用投票的方式來決定產品在人們之間的分配。投票方式,從最根本上著眼,是人類社會內部成員選擇和決定人類社會內部事務的方法。而正是採用這種形式進行的選擇和決策,卻可忽略了人類生存的必要前提:即人類社會的整個存在,不僅僅決定於內部成員的主觀意願,還決定於人類社會生存於斯的自然界。
福利函數的投票決定,在某種意義上看,就是人們希望擺脫自然通過生產函數和派生的分配函數對於人們的強制分配作用,純粹由人們之間協商與協調,對人們的收入進行內部分配。但是,這樣決策卻很可能是無約束的決策,或者準確地說是自由度過多的決策。仁者見仁,智者見智,得不到唯一結果就不難理解。正像沒有分配函數作用時的帕累托最優狀態無法獲得唯一解一樣,人們看到了同樣的問題出現在它的反面:在投票選擇中,人們也無法獲得公平分配的唯一解,即沒有全體人們同時滿意的公平解。
回過頭來,從經濟學的分析脈絡看貨幣選票的真實作用,它絕不僅僅直接安排與解決了人與人之間的利益調節分配關係,它還間接地安排與解決了人從自然中如何獲得利益的關係。貨幣投票安排著三個邊際代替率相同,不但解決了人類社會內部的協調關係,更考慮了人與自然的互相作用和影響的機理。所以,貨幣投票選擇絕不等同於政治投票選擇。
阿羅投票悖論的出現,其最根本的深層原因就在於:由於沒有充分的約束,即當自然約束缺位時,就無法就人類事務達成唯一解。這就是阿羅悖論的深層機制起源。
阿羅不可能定理的證明並不難,但是需要嚴格的數學邏輯思維。關於這個定理還有一段情節頗為曲折的故事。

阿羅悖論
後來,阿羅考上研究生.在霍特林·哈羅德(Harold Hotelling)的指導下攻讀數理經濟學。他發現,邏輯學在經濟學中大有用武之地。就拿消費者的最優決策來說吧,消費者從許多商品組合中選出其最偏好的組台、這正好與邏輯學上的排序概念吻台。又如廠商理論總是假設廠商追求利潤最大化,當考慮時間因素時,因為將來的價格是未知的廠商只能力圖使基於期望價格的期望利潤最大化。
我們知道、現代經濟中的企業一般是由許多股東所共同擁有。100個股東對將來的價格可能有100種不同的期望,相應地根據期望利潤進行諸如投資之類的決策時便有100種方案。那末,問題如何解決呢?一個自然的辦法是由股東(按其佔有股份多少)進行投票表決,得票最多的方案獲勝。這又是一個排序問題。阿羅所受的邏輯訓練使他自然而然地對這種關係的傳遞性進行考察。結果輕而易舉地舉出了一個反例。
阿羅第一次對社會選擇問題的嚴肅思考就這樣成為他學習標準廠商理論的一個副產品不滿足傳遞性的反例激起了阿羅的極大興趣,但同時也成為他進一步研究的障礙 因為他覺得這個悖論素未謀面但又似曾相識。事實上這的確是一個十分古老的悖論,是由法國政治哲學家、概率理論家貢多賽在1785年提出的 但是阿羅那時對貢多賽和其他原始材料一無所知,於是暫時放棄了進一步的研究。這是1947年。
次年,在芝加哥考爾斯(Cowles)經濟研究委員會,阿羅出於某種原因對選擇政治學發生了濃厚的興趣:他發現在某些條件下,“少數服從多數”的確可以成為一個合理的投票規則。但是一個月後,他在《政治經濟學雜誌》里發現布萊克(Black)的一篇文章已捷足先登,這篇文章表達了同樣的思想看來只好再一次半途而廢了。阿羅沒有繼續研究下去其實還有另一層的原因,就是他一直以嚴肅的經濟學研究為己任,特別是致力於運用一般均衡理論來建立一個切實可行的模型作為經濟計量分析的基礎他認為在除此以外的“旁門左遭’中深究下去會分散他的精力。
1949年夏天,阿羅擔任蘭德公司(Rand)的顧問。這個為給美國空軍提供諮詢而建立起來的公司那時的研究範圍十分廣泛,包括當時尚屬鮮為人知的對策論。職員中有個名叫赫爾墨(]Helmer) 的哲學家試圖將對策論應用於國家關係的研究,但是有個問題令他感到十分棘手:當將局中人詮釋為國家時,儘管個人的偏好是足夠清楚的,但是由個人組成的集體的偏好是如何定義的呢?阿羅告訴他,經濟學家已經考慮過這個問題,並且一個恰當的形式化描述已經由伯格森(Bergson)在1938年給出。伯格森用一個叫做社會福利函數的映射來描述將個人偏好彙集成為社會偏好的問題,它將諸個人的效用組成的向量轉化為一個社會效用。雖然伯格森的敘述是基於基數效用概念的,但是阿羅告訴赫爾墨,不難用序數效用概念加以重新表述。於是赫爾墨順水推舟,請阿羅為他寫一個詳細的說明當阿羅依囑著手去做時,他立即意識到這個問題跟兩年來一直困擾著他的問題實際上是一樣的。既然已經知道“少數服從多數“一般來說不能將個人的偏好彙集成社會的偏好,阿羅猜測也許會有其他方法。幾天的試探碰壁之後,阿羅懷疑這個問題會有一個不可能性的結果。果然,他很快就發現了這樣一個結果;幾個星期以後,他又對這個結果作進一步加強。
阿羅不可能定理就這樣呱呱墜地了。
從1947年萌發胚芽到1950年開花結果,阿羅不可能定理的問世可謂一波三折,千呼萬喚始出來,而且頗有點無心插柳的意味。但是,正是在這無心背後的對科學鍥而不捨的追求,才使邏輯學在社會科學這塊他鄉異壤開出一朵千古留芳的奇葩,這不能不說是耐人尋味的。
1951年,阿羅出版了現在已經成為經濟學經典著作之一的《社會選擇與個人價值》一書。
對於阿羅不可能定理,美國斯坦福大學教授肯尼斯·阿羅給出了如下的結論:
如果我們排除了人際效用的可比性,而且在一個相當廣的範圍內對任何個人偏好排序集合都有定義,那麼把個人偏好總合為社會偏好的最理想的方法,要麼是強加的,要麼是獨裁的。不可能存在一種社會選擇機制,使個人偏好通過多數票規則轉換為成社會偏好。
阿羅的不可能定理源自孔多塞。康德爾塞(Coudorcet,Marquis de)的“投票悖論”。早在十八世紀法國思想家孔多塞。康德爾塞就提出了著名的“投票悖論”:假設甲乙丙三人,面對ABC三個備選方案,有如下的偏好排序。
阿羅悖論
乙(b > c > a)
丙(c > a > b)
註:甲(a > b > c)代表——甲偏好a勝於b,又偏好b勝於c。
1.若取“a”、“b”對決,那麼按照偏好次序排列如下:
甲(a > b )
乙(b > a )
丙(a > b )
社會次序偏好為(a > b )
2.若取“b”、“c”對決,那麼按照偏好次序排列如下:
甲(b > c )
乙(b > c )
丙(c > b )
社會次序偏好為(b > c )
3.若取“a”、“c”對決,那麼按照偏好次序排列如下:
甲(a > c )
乙(c > a )
丙(c > a )
社會次序偏好為(c > a )
於是我們得到三個社會偏好次序——(a > b )、(b > c )、(c > a ),其投票結果顯示“社會偏好”有如下事實:社會偏好a勝於b、偏好b勝於c、偏好c勝於a。顯而易見,這種所謂的“社會偏好次序”包含有內在的矛盾,即社會偏好a勝於c,而又認為a不如c!所以按照投票的大多數規則,不能得出合理的社會偏好次序。
阿羅不可能定理說明,依靠簡單多數的投票原則,要在各種個人偏好中選擇出一個共同一致的順序,是不可能的。這樣,一個合理的公共產品決定只能來自於一個可以勝任的公共權利機關,要想藉助於投票過程來達到協調一致的集體選擇結果,一般是不可能的。
為了簡單起見,假定每個個體至少有3個供排列的選項,可以用各種味道的餅乾為選項的例子,如:香草餅乾(V)、巧克力餅乾(C)和草莓餅乾(S),每一個人要形成一個序列,表示出他對3種味道的喜愛程度,如V>S>C,表示這個人最喜歡香草餅乾,其次是草莓餅乾,最後是巧克力餅乾。設有甲乙丙三人作選擇,他們的個人偏好為:
甲: V>C>S
乙: C>S>V
丙: S>V>C
表1 投票悖論
| 投票者 | 對不同選擇方案的偏好次序 | ||
| 甲 | V | C | S |
| 乙 | C | S | V |
| 丙 | S | V | C |
用民主的多數表決方式,如果三個人都能充分表達自己的意見,則結果必然如下所示:
a. 首先,在V和C中選擇,甲、丙喜歡V,乙喜歡C;
b. 然後,在C和S中選擇,甲、乙喜歡C,丙喜歡S;
c. 最後,在V和S中選擇,乙、丙喜歡S,甲喜歡V。
這樣三個人的最終表決結果如下:
V>C,C>S,S>V可見,利用少數服從多數的投票機制,將產生不出一個令所有人滿意的結論,這就是著名的“投票悖論”(paradox of voting)。
用數學語言來說,即:假設群體S上有m個個體成員,群體中出現的各種事件構成一個集合X,每個個體對每一事件都有自己的態度,即每個人都對集合X有一個偏好關係> i=1,2,…,m。即可以按自己的偏好為事件排序。定義群體的偏好為:其中P是一種由每個個體偏好得出群體偏好的規則。按這個規則從個體排序(偏好)得到群體排序(偏好),而且這個排序符合民主社會的民主決策的各種要求。注意這個排序是自反的,即如果A>B,那麼,B表述出這些要求。他用的是數學方法,符號化的公理和數理邏輯的證明方法,為了簡單地說明問題,我們採用了自然語言解釋。)分為兩條1條,把公理5有時表述為(個公理4,二者只有其一而且必有其一。這首先要考察一下民主社會的民主決策的各種要求是什麼,阿羅用B>A,要麼A>B;並且還是完全的,即要麼A>C,則有B>C,A>B;是可傳遞的,即如果
公理1——個體可以有任何偏好;而且是民主選擇——每個社會成員都可以自由地按自己的偏好進行選擇(數學上稱為原則U—無限制原則: > i,u=1,2,… , m在x上的定義方式無任何限制)。
公理2 ——不相干的選擇是互相獨立的;(數學上稱為原則I— 獨立性原則:對於X中的兩個事件X和Y,對它們做出的偏好判斷與X中的任何其他事件無關)。
公理3 ——社會價值與個體價值之間有正向關聯;(數學上稱為原則P—一致性原則:如果對X中的兩個事件X和Y,對於所有的i都有x < iY,那麼X < sY。這裡x < iY表示X> iY不成立。就是說,每人都有同樣明確態度的兩件事,社會也應該有同樣的態度。)
公理4 ——沒有獨裁者—不存在能把個體偏好強加給社會的可能。(數學上稱為原則D—非獨裁原則:不存在某個i,使得。
阿羅證明,滿足這4條公理表述的要求的民主決策的規則是不存在的,就是著名的“阿羅不可能性定理”:如果X中的事件個數不小於3,那麼就不存在任何遵循原則U,P,I,D的規則(稱“社會福利函數”)。這表明滿足所有一般條件的民主選擇要麼是強加的,要麼就是獨裁的結果。
換句話說,阿羅不可能性定理指出,多數規則(majorily rule)的一個根本缺陷就是在實際決策中往往導致循環投票。
阿羅的結論是:根本不存在一種能既保證效率、尊重個人偏好、並且不依賴? 那麼,能不能設計出一個消除循環投票,做出合理決策的投票方案呢程序(agenda)的多數規則的投票方案。簡單地說,阿羅的不可能定理意味著,在通常情況下,當社會所有成員的偏好為已知時,不可能通過一定的方法從個人偏好次序得出社會偏好次序,不可能通過一定的程序準確地表達社會全體成員的個人偏好或者達到合意的公共決策。
這個結果是令人震動的:一個社會不可能有完全的每個個人的自由—— 否則將導致獨裁;一個社會也不可能實現完全的自由經濟—— 否則將導致壟斷。人們對社會的認識達到一個新的高度。
阿羅的不可能定理一經問世便對當時的政治哲學和福利經濟學產生了巨大的衝擊,甚至招來了上百篇文章對他的定理的駁斥。李特爾、薩繆爾森試圖以與福利經濟學不相干的論點來駁倒阿羅的不可能定理,但又遭到肯普、黃有光和帕克斯的反駁,他們甚至建立了在給定個人次序情況下的不可能性結果。
事實上,阿羅不可能性定理經受住了所有技術上的批評,其基本理論從來沒有受到重大挑戰,可以說是無懈可擊的,於是阿羅不可能定理似乎成為規範經濟學發展的一個不可逾越的障礙。怎樣綜合社會個體的偏好,怎樣在理論上找到一個令人滿意的評價不同社會形態的方法,成為一個世界性難題。這時候出現了阿馬弟亞·森(Amartya Kumar Sen,1933一)從20世紀60年代中期起,森在工具性建設方面的貢獻減少了這種悲觀主義色彩。森在這方面的研究推動了規範經濟學跨越這個障礙向前發展。他的研究工作不僅豐富了社會選擇理論的原則,而且開闢了一個新的、重要的研究天地。森1970年的著作《集體選擇和社會福利》是其最重要的一部著作,它使許多研究者恢復了對基本福利的興趣。另外這本書還具有哲學的風格,為規範問題的經濟分析提供了一個新的視角,克服了阿羅不可能定理衍生出的難題,從而對福利經濟學的基礎理論作出了巨大的貢獻。
森所建議的解決方法其實非常簡單。森發現,當所有人都同意其中一項選擇方案並非最佳的情況下,阿羅的“投票悖論”就可以迎刃而解。比如,假定所有人均同意V項選擇方案並非最佳,這樣上面的表1就變為表2,僅僅甲的偏好由於同意“V並非最佳”而V和C的順序互換了一下,別的都不變。
表2 投票悖論的解決
| 投票者 | 對不同選擇方案的偏好次序 | ||
| 甲 | C | V | S |
| 乙 | C | S | V |
| 丙 | S | V | C |
在對V和C兩種方案投票時,C以兩票(甲乙)對一票(丙)而勝出於V(C>V);同理,在對V和S以及C和S分別進行投票時,可以得到S以兩票(乙丙)對一票(甲)而勝出於V(S>V);C以兩票(甲乙)對一票(丙)而勝出於S(C>S)。這樣,C>S—S>V—C>V,投票悖論就此宣告消失,唯有C項選擇方案得到大多數票而獲勝。
森把這個發現加以延伸和拓展,得出了解決投票悖論的三種選擇模式:
(1)所有人都同意其中一項選擇方案並非最佳;
(2)所有人都同意其中一項選擇方案並非次佳;
(3)所有人都同意其中一項選擇方案並非最差。
森認為,在上述三種選擇模式下,投票悖論不會再出現,取而代之的結果是得大多數票者獲勝的規則總是能達到唯一的決定。
一個更完整、更簡單也更具一般意義的不可能性定理,是艾利亞斯在2004年發表的。這一定理聲稱:如果有多於兩個可供選擇的社會狀態,那麼,任何社會集結運算元,只要滿足“偏好逆轉”假設和“弱帕累托”假設,就必定是獨裁的。特別地,阿羅的社會福利函數和森的社會選擇函數,都是社會集結運算元的特例,並且偏好逆轉假設在阿羅和繆勒各自定義的社會選擇框架內分別等價於阿羅的“獨立性假設”和繆勒的“單調性假設”,從而阿羅的不可能性定理、森的最小自由與帕累托效率兼容的不可能性定理、繆勒和塞特斯維特的一般不可能性定理,均可視為艾利亞斯一般不可能性定理的特例。艾利亞斯的不可能性定理有怎樣的經濟學和社會學結論是人們正在研究的問題。
1. 公平與效率相悖
公平與效率相悖是阿羅悖論的一個應用側面。有了對阿羅悖論的這樣理解,回過頭來再分析公平與效率的相悖性,問題豁然開朗。
從古代臆想中的“大同”社會,延至近代觀念的“烏托邦”社會,直到現代的實際性的社會主義社會,檢驗社會經濟狀況好壞標準,始終貫穿著一條主線,就是“公平”。但是,“公平”這一尺度來自何處,在福利經濟學通過效率轉而對它進行認真研究之前,一直為人們所漠視。

阿羅悖論圖片
但與此同時,當人們在追求美好生活過程中,又總是發現僅僅用“公平”尺度來衡量遠遠不夠,必須導入“效率”尺度與之互補。而“效率”尺度衡量的東西就不再完全是人類的社會內部事務,它還必然牽涉到人與自然的索取與利益的關係。
“公平”尺度的對偶物——“效率”尺度,自帕累托始開始準確引入,為西方經濟學者一直堅持並用之檢驗社會經濟狀況好壞的標準。然而,由福利經濟學發展結果來看,“效率”尺度決不能囊括全部,它的實施,還必須引入“公平”尺度與之互補。
這就是“效率”與“公平”的悖論。強調“效率”尺度時,就會引入“公平”尺度;反之,強調“公平”尺度時,又會引入“效率”尺度。堅持了其中任何一個,都會把另一個拖進來。兩者似乎不能兩全其美,但又必需兩相照顧。兩者既無法分開,又無法綜合,似乎是統一體中的矛盾對立面。
學術史實還表明,當用投票或者其它的方式決定公平分配方式的同時,卻又引進了巨大的弊端。由於生產過程同時就是再生產過程,人們還必須在現時的消費與將來的消費之間進行決策。已經發現,用人們內部協商或者投票等方式決定的分配,在改變了現時消費於人們之間分配的同時,也會改變生產要素的報酬比例,即“自然”機制決定的現時消費與將來消費之間的適當關係。因為,人類的生存環境,已不再是純粹的自然,而是人造的自然。這種人造的自然,必須以人們不斷地維護和改進才能保持。而維護和改進與生產要素的回報有著直接的關係。投票選擇分配的結果肯定會改變生產要素的回報。而真正要命的是,這樣的改變,總是使得下一回合的再生產,偏離帕累托最優狀態。這意味著在公平地切割已生產蛋糕的同時,卻將使得再生產出來的蛋糕變小。
那麼,是否可由經濟體系運行內部,得出同時兼顧“效率”與“公平”尺度的結論呢?因為,我們已經看到,光考慮“效率”,並無法得到經濟運行的唯一解,光考慮“公平”,也無法得到經濟運行唯一解,綜合考慮兩者,是否存在著一組解,能夠同時獲得滿足“效率”與“公平”尺度,即是:在效率最大的同時,達到公平最佳。
可以!因為我們已經看到,一旦加入自然界對人類社會存在的約束后,則由於新的約束進入,得到唯一結果就有其存在的必然。至於這個結論的證明,請看筆者近期將發表的其它論文。在那裡,會給出一個時時刻刻保持自然的約束下,得到效率最大同時公平最佳的結論。這就使得當我們評價任何一個真實經濟體系運行時,可以有一個“效率”與“公平”兼顧的坐標系,以便讓人們判斷、衡量實際經濟運行偏離這兩把理想尺度的尺寸偏差。
然而遺憾的是,這樣的自然約束全面在位曾經出現過,它使得人們生活在即“公平”又有“效率”的社會中,不過它僅出現在人類的幼年時期——原始社會中。那時由於生產力的極其低下,任何偏離“公平”的分配,都會使某些人得不到足夠食物而死亡。自然的在位就是以殘酷的面目迫使人們不但進行“效率”地生產,而且強迫進行“公平”地分配。
然而,當生產力提高以至人們有了“剩餘”產品后,分配的自由度增大,自然的約束不再那麼嚴厲,使得阿羅悖論不但在“效率”方面,而且在“公平”方面都有了生存餘地。
2. 社會主義市場經濟的確立
社會主義市場經濟的確立是阿羅悖論獨裁結論的應用。
阿羅投票悖論中邏輯地推出的結果,卻令人觸目驚心:社會的決定要麼是外界強加的,要麼是獨裁作出的。
他的話一半正確,另一半有疑問。說對的一半是,決定必定要由外界強加,即由人類以外的因素強加,這反映了自然約束的複位。它印證了存在著人無法脫離生存於斯的自然,就像人無法抓住自己頭髮脫離地球一樣。另一半話則值得深思,即決定必需是獨裁的。我們得有前提地承認這樣的結論,因為確實存在著由全體人的理性投票無法獲得的結果,居然可由獨裁的決策獲得。但如對這一半話濫用,將會造成極其嚴重的災難性後果。
然而,通過以上闡述明白阿羅投票悖論的來源后,對於社會決策的決定機理,就有進一步的深刻理解。因為,不管怎麼說,社會決策畢竟是在社會內部作出的,雖然它仍需體現自然的約束,比如當應用貨幣選票時。但是,貨幣選票只是社會決策的一種方式,雖然它是一種極其重要的方式,社會決策還存在著不能用貨幣選票決定內容。而由阿羅悖論,對這些內容進行的決策,絕對無法排除獨裁的因素。那麼,獨裁決定的方式與自然的外加約束兩者又有什麼關係呢?這在下面的由交易費用考慮引發的中國社會主義市場經濟的確立中加以分析。
自蘭格等人對社會主義計劃經濟如何實施最優配置進行分析后,人們已清晰地認識到,經濟體系的運行並非不要代價,資源的配置和產品的分配是需要成本的。但是,這樣的代價和成本如何進入經濟分析的視野,卻有賴於科斯提出的“交易費用”。科斯深入思考了前人忽略了的交易如何進行和獲得的問題,發現市場交易中必然存在著的成本——交易費用。從這一縫隙的微光中,發現了一個廣闊的新天地。
在這束螢光微芒指導下經長期的探索,人們最終恍然大悟,得出了這樣的結論:人類的生存形式之所以會演變成現在的市場價格體系,用它來解決人類社會生存中的人與人之間的信息傳導、生產協作、資源配置與物品交換,從而解決人類整體向大自然進行最有效率的索取,是因為市場價格體系是一種費用最低的體系,套用力學的語言,它是一種磨擦係數最低的體系。
以交易費用為發端,新制度學派從中引申出了對於產權、社會意識形態、法律、政府、民主等上層建築的研究和論證,發現了所有為經濟制度運行的社會活動,都是有費用的。
從而,新制度學派們從唯物的角度恢復了社會研究中的政治經濟學。這也從另一個方面印證了馬克思主義經濟學的長處。然而,對比起來,它甚至比經典的馬克思主義經濟學要更唯物一些。因為,馬克思的經典經濟學從勞動價值論入手,分析社會中由於經濟關係連接而形成的人與人之間的社會關係,並專註於社會關係,從中引申出對於上層建築的研究。可是,由於前提所限,視野所及,無法納入經濟基礎研究中必然需涉及的資源最優配置。這是它的理論盲點。新制度學派們的研究在這個意義上,添補了馬克思經典經濟學的不足,真正從經濟基礎論證了上層建築的產生和存在是為經濟基礎服務的,同時,也正是這些經濟基礎,以形似交易費用的這樣那樣的成本開支,支撐著上層建築的運行。
理解這些后,對於人類社會決策行為就有了一個更堅實的、更唯物的思考基石。
一個好的“獨裁”決策,不但應使人們的生產消費範圍達到最大的邊緣地區,也應保障社會內部正常運行費用降至最低限度。開“源”節“流”,才能得到所謂的經濟術語的效率最高境界,或者說是考慮了“磨擦力”后的帕累托最優狀態。
做出這樣的決策決不是一蹴而就的事。有時,為了獲得這樣的“獨裁”決策,得通過長時期的,甚至是成本高昂、代價痛苦的摸索。
中華人民共和國成立后,隨著革命戰爭的結束,驟風暴雨般的階級鬥爭本也應隨之趨緩,而解決低下的人民生活水平、發展落後的民族經濟和建設現代化強國則成為當務之急。然而,黨的中心工作卻長時期偏離了發展國民經濟這一目標。“十年動亂”結束之後,中國共產黨開始清醒地意識到,必須堅定不移地把黨的中心工作放在經濟建設上,而不為任何干擾所動搖。就是這個決策,為中國的經濟起飛奠定了思想基礎。
確定以經濟建設為中心,解決了方向問題,而以什麼樣的體制來實現經濟建設,則是途徑問題。在此問題上,中國共產黨也經過了相當長時期的摸索。從拋棄傳統的計劃經濟,實施有計劃的市場經濟,到後來提計劃經濟與市場經濟相結合,一直到黨的十四大,才確定建立社會主義市場經濟。這個過程大致用了了15年。
市場經濟中的生產主體是企業。對於公有制於企業中如何實施的問題,也通過長期的理論爭論和實踐實驗,於黨的十五大才明確地提出了它的實現途徑。這個過程如果從1992年算起的話,大致也經過了5 年左右時間。實際上,就簡政放權,實施承包制開始算起,一直可以追溯到1984年。
從整體上說,從認識到市場經濟是一種效率最高、運行費用最低經濟制度,到最終決定採用市場經濟作為實施現代中國騰飛的手段,整整耗費了將近半個世紀時間。
另外,降低社會運行的成本費用,雖然不是在有清晰意識和理論指導的情況下進行的,但中國共產黨是成熟的執政黨,政治領袖是睿智的,相當清楚中國近代史上內亂不止、積貧積弱的現象,且又從“文化大革命”吸取了教訓,因而能夠從政治穩定的視角思考中國的經濟轉軌問題。
與俄羅斯相比,由於它們輕率地採取了所謂的“休克”療法來進行經濟制度轉型,“畢其功於一役”,其費用實在過於高昂。現在比較一致的認識是:應該在保持政治穩定局面的同時,建立和維護市場經濟法制,逐步轉軌。
這些決策雖然並非是全民投票的結果,而是執政黨的政治決定,但它們反映了人民的迫切願望,也反映了自然對於人類的約束作用。這也是中國共產黨理論思維水平高超與政治決策成熟的表現。
3. 公共選擇與民主制度
阿羅悖論
大致說來,經濟個體在市場條件下作出的決策,都是私人選擇,而公共選擇則大量地發生在政治領域,如制定或修改法律,選舉政府官員,充實國防力量等等。經濟學有一個分支——公共選擇理論,專門來分析上述發生在政治領域中的決策行為,阿羅不可能性定理就是有關決策效果的一個重要結論。
市場條件下的私人選擇,實際上是經濟個體利用自己手中的“貨幣選票”,直接地表達他們對各種產品的意見。對於這種行為的研究,一直是經濟學的核心內容。比較一致的結論是,市場條件下的私人選擇,通常可以導致有效率的結果,能夠引導資源實現合理配置,但也存在著市場失靈的情況。而在政治領域中,個人意願的表達,必須經過公共選擇這個過程,在民主制度下,最為常見的辦法就是投票。那麼,它是否也能導致一種有效率的結果呢?這便跟投票的規則有很大的關係。
公共選擇理論的創始人布坎南認為,一致同意規則是公共選擇的最高準則。“任何一個有理性的人都不會同意那些預期會給他帶來損害的事情”,因此,一個人一旦同意了某一選擇,他一定認為這是對他有利的,至少不會受損。市場機制之所以有效,就是因為在市場中達成的任何一筆交易,都是以交易雙方的一致同意為基礎的,哪怕有一方不同意,交易都無法達成。這一原則對公共選擇來說也是適用的,只要某一集體決策獲得了一致同意,那就表明,它肯定沒有使任何一個參與者受損,卻至少對其中的一個人有利。用經濟學的術語來說,這就是一種帕累托效率的改進。
然而令人遺憾的是,“一致性是件好事,但卻太昂貴了”。各參與者之間的利益差別不可避免,而每項議案的通過,卻都要徵得所有人的同意,這就需要付出巨大的努力,去說服每一個人,直至最後一個懷疑者。更糟糕的是,一旦這個最後的懷疑者認識到他有如此巨大的威力,他就有可能以投否決票相要挾,去敲詐那些支持議案的人。通常的情況則是,在馬拉松式的討價還價中,達不成任何協議。
既然一致同意規則代價高昂,人們就轉而求其次,降低同意的“百分比”,將一致同意的100%,降為80%、70%,或者是51%,這樣就產生了多數同意規則。相對於一致同意來講,多數同意規則無疑是降低了決策的成本,但由於每項決策都可能在有人反對的情況下通過,這就便公共選擇帶有了強制的色彩。儘管作為一個和平主義者,你不贊成軍備擴張,但卻必須跟那些鷹派人物一樣,為擴張軍備而納稅,為別人的選擇支付成本。對此,人們通常的看法是,少數服從多數是一種“民主”的公共選擇過程,它雖然使少部分人受損,但同時卻讓大部分人獲益。因此,從整個社會的角度看,這個決策還不失為一個“好”的決策。
問題在於,“民主”並非真的萬無一失。例如:
某日,人們舉辦一個投票,這個投票問卷里只有一個問題,包含若干個選項,投票者根據自己的偏好給這幾個選項排序。人們希望滿足以下幾個條件:
——投票的結果應該能表現出多個參加者的偏好,而不是某個人的偏好。
——它應該能體現所有參加者的偏好,並且如果有2次投票所有人投的票相同,結果也一定相同。
——如果人們改變了某2個選項的相對優先順序,那麼這變化不應該影響其它選項的相對優先順序。
——如果一個人提高了某個選項的優先順序,那麼在結果中,這個選項的優先順序不能因此下降。
——所有結果的排序都應該是可能達到的。
有 N 種選擇,有 m 個決策者,他們每個人都對這 N 個選擇有一個從優至劣的排序。我們要設計一種選舉法則,使得將這 m 個排序的信息匯總成一個新的排序,稱為投票結果。我們希望這種法則滿足以下條件:
a. 一致性,或稱為帕累托效率。即如果所有的 m 個決策者都認為選擇 a 優於 b,那麼在投票結果中,a 也優於 b。
b. 非獨裁。不存在一個決策者 X,使得投票結果總是等同於 X 的排序。
c. 獨立於無關選項。如果現在一些決策者改了主意,但是在每個決策者的排序中,a 和 b 的相對位置不變,那麼在投票結果中 a 和 b 的相對位置也不變。
循環投票現象最早是由法國人孔多塞特發現的,後來美國經濟學家阿羅又進行了更進一步的研究。他發現,如果兩個以上的投票者,就兩個以上的方案進行表決,循環投票就總有可能出現,出現的概率隨著投票人數和供選方案的增多而增大。在此基礎上,阿羅經過嚴格的數學證明,得出了一個令人吃驚的結論:任何一種多數同意規則,都不可能萬元一失的保證投票的結果符合大多數人的意願。阿羅的結論是,如果有2個或以上的人參加投票,並且問題有3個或以上的選項,那麼以上的這些條件不可能同時滿足。也就是說,如果m大於2, N 大於 3,我們不可能設計出這種制度。這就是著名的阿羅不可能性定理,又稱阿羅悖論。
阿羅悖論使我們對公共選擇和民主制度有了新的認識,正如市場存在著失靈一樣,民主也有它失效的時候。儘管失效的概率可能很小,但這並不意味著阿羅的警告無足輕重。飛機失事只有不足萬分之一的可能,但它一旦掉下來,對乘客來說就是百分之百的災難。
