雙線性變換法
雙線性變換法
雙線性變換法的主要優點是S平面與Z平面一單值對應,S平面的虛軸(整個jΩ)對應於Z平面單位圓的一周,S平面的Ω=0處對應於Z平面的ω=0處,對應即數字濾波器的頻率響應終止於折迭頻率處,所以雙線性變換不存在混迭效應。
脈衝響應不變法的主要缺點是頻譜交疊產生的混淆,這是從S平面到Z平面的標準變換z=e的多值對應關係導致的,為了克服這一缺點,設想變換分為兩步。
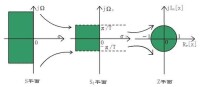
雙線性變換法的映射關係
通過標準變換關係將此橫帶變換到整個Z平面上去。
由此建立S平面與Z平面一一對應的單值關係,消除多值性,也就消除了混淆現象。
為了將s平面的jΩ軸壓縮到s1平面jΩ軸上的一段上,可通過以下的正切變換實現。
這裡C是待定常數,下面會講到用不同的方法確定C,可使模擬濾波器的頻率特性與數字濾波器的頻率特性在不同頻率點有對應關係。
上面講到,用不同的方法確定待定常數C,可以使模擬濾波器的頻率特性與數字濾波器的頻率特性在不同頻率點有對應關係。也就是說,常數C可以調節頻帶間的對應關係。
①保證模擬濾波器的低頻特性逼近數字濾波器的低頻特性。此時兩者在低頻處有確切的對應關係,即
因為Ω和ω都比較小。
另外,根據歸一化數字頻率ω與模擬頻率Ω的關係,所以有Ω=cΩT/2,所以,c=2/T
②保證數字濾波器的某一特定頻率,如截止頻率,與模擬濾波器的某一待定頻率Ωc嚴格對應。
與脈衝響應不變法相比,雙線性變換的主要優點:靠頻率的嚴重非線性關係得到S平面與Z平面的單值一一對應關係,整個jΩ軸單值對應於單位圓一周,這個關係就是式 所表示的,其中ω和Ω為非線性關係。如圖圖中看到,在零頻率附近,Ω~ω接近於線性關係,Ω進一步增加時,ω增長變得緩慢,(ω終止於摺疊頻率處),所以雙線性變換不會出現由於高頻部分超過摺疊頻率而混淆到低頻部分去的現象。
雙線性變換法的缺點:Ω與ω的非線性關係,導致數字濾波器的幅頻響應相對於模擬濾波器的幅頻響應有畸變,(使數字濾波器與模擬濾波器在響應與頻率的對應關係上發生畸變)。例如,一個模擬微分器,它的幅度與頻率是線性關係,但通過雙線性變換后,就不可能得到數字微分器。
另外,一個線性相位的模擬濾波器經雙線性變換后,濾波器就不再有線性相位特性。雖然雙線性變換有這樣的缺點,但它目前仍是使用得最普遍、最有成效的一種設計工具。這是因為大多數濾波器都具有分段常數的頻響特性,如低通、高通、帶通和帶阻等,它們在通帶內要求逼近一個衰減為零的常數特性,在阻帶部分要求逼近一個衰減為∞的常數特性,這種特性的濾波器通過雙線性變換后,雖然頻率發生了非線性變化,但其幅頻特性仍保持分段常數的特性。
雙線性變換比脈衝響應法的設計計算更直接和簡單。由於s與z之間的簡單代數關係,所以從模擬傳遞函數可直接通過代數置換得到數字濾波器的傳遞函數。