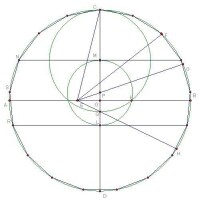
正十七邊形
德國高斯提出的幾何學術語

正十七邊形
高斯(1777─1855年)德國數學家、物理學家和天文學家。高斯在童年時代就表現出非凡的數學天才。年僅三歲,就學會了算術,八歲因運用等差數列求和公式而深得老師和同學的欽佩。大學二年級時得出正十七邊形的尺規作圖法,並給出了可用尺規作圖的正多邊形的條件。解決了兩千年來懸而未決的難題,1799年以代數基本定理的四個漂亮證明獲博士學位。高斯的數學成就遍及各個領域,在數學許多方面的貢獻都有著劃時代的意義。並在天文學,大地測量學和磁學的研究中都有傑出的貢獻。
先計算或作出
設正17邊形中心角為a,則,即
故,而
因不等於0,兩邊除之有:
又由(三角函數積化和差公式)等
注意到(誘導公式)等,有
令
有:
又
=
經計算知
因而:,
其次再設:
故有
最後,由
可求cosa之表達式,
它是有理數的加減乘除平方根的組合, 故正17邊形可用尺規作出
做法
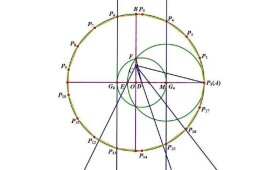
正十七邊形
2.在OA上作E點使,連結CE.
3.作∠CEB的平分線EF.
4.作∠FEB的平分線EG,交CO於P.
5.作,交CD於Q.
6.以CQ為直徑作圓,交OB於K.
7.以P為圓心,PK為半徑作圓,交CD於L、M.
8.分別過M、L作CD的垂線,交圓O於N、R.
9.作弧NR的中點S,以SN為半徑將圓O分成17等份.
因為,利用可得近似角。用該方法作正十七邊形總誤差為,在不要求十分精確的情況下還是可行的。
作法如下:
1.先畫一條直線,用圓規在上面截取5條相等線段,(盡量越短越好),再截取之前四條線段的和,接續之前畫的線段。這樣,如果每條小線段算作0.1的話,那麼整條線段就是1.8。
2.用圓規截取之前5條小線段的長,畫5次,這樣這條線段就是5。。準備工作完畢!
3.另作一條直線,作垂線,1.8的線段作為對邊,5的線段作為斜邊,那個最小的銳角即是近似的的角。以其頂點為圓心,重複作角直至閉合。畫一大圓,連接其與17條射線的交點,即可。