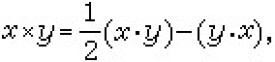非結合代數

一般環論中的一個分支，與結合代數在方法和內容上都有非常密切的聯繫。從結合代數的定義中把乘法適合結合律這一條件刪去，就是非結合代數的定義。李代數、若爾當代數、交錯代數，以及李型代數、若爾當型代數都是非結合代數最重要的類型。非交換若爾當代數、右交錯代數、交錯李代數、馬爾采夫代數、冪結合代數則是李代數、交錯代數或若爾當代數的推廣。非結合代數中的乘法往往滿足某些恆等式。

李代數是一種非結合代數，其乘法滿足恆等式:。在一個域F（特徵非2）上結合代數〈A,+,·〉中，將原來的有結合律的乘法·換成新引入的乘法×：

得到的〈A，＋，×〉就是一個李代數。由結合代數A如此得來的李代數，記作A_。

若爾當代數是20世紀30年代P.若爾當、J.馮·諾伊曼和E.威格納等人，在研究量子力學的基礎時引用的一種非結合代數。在描述量子力學基礎時涉及結合代數〈A，＋,·〉（希爾伯特空間的運算元代數）中，將原來的有結合律的乘法·換成新的乘法。：

就得到非結合代數〈A，+，。〉，其中乘法。滿足恆等式和，這裡；後來，就把滿足這兩個恆等式的代數稱為若爾當代數, 並將如此得出的若爾當代數記作 A+。之所以規定乘法。如(2)，是因為考慮到：若x、y都是埃爾米特運算元，則x。y也是埃爾米特運算元，但一般說來，x·y已不是埃爾米特運算元。

李型代數和若爾當型代數的概念，早在20世紀40年代末期就由A.A.阿爾貝特提出來了，但它的重要性還是自70年代以來由於理論物理的需要，例如在統計物理、力學、原子物理中討論無勢相互作用等，才顯示出來。所謂一個代數〈A,+,·〉為李型代數，是指〈A，+,×〉是李代數，其中新乘法×由(1)定義。結合代數和李代數都是李型代數。所謂一個代數〈A,+,·〉為若爾當型代數，是指〈A,+,。〉是若爾當代數，其中新乘法。由(2)定義。結合代數和交錯代數都是若爾當型代數。

交錯代數的產生是由於推廣數系。令Q表實數域R上四元代數。它是可除結合代數，取其標準基1,i,j,k,則Q中元素 α有惟一的表示式。再定義α的共軛元為 則α→是Q的一個對合，且有。所謂Q的一個對合，是指Q 的反自同構，且其平方等於恆等自同構。

仿照由複數作四元數的方法，用四元數來構造八元數即凱萊數。令C是一切四元數對(α,b)的集合，規定其運算：這裡分別是с、d的共軛元,。由直接驗證可知，C 是實數域R上的8維代數，有單位元(1,0)。它是可除代數，即對於任意，在C 中和有解。它的乘法不適合結合律，卻滿足恆等式和 。把滿足這兩個恆等式的代數稱為交錯代數。凱萊代數是交錯可除代數的一個例子。結合代數是交錯代數。刻畫交錯代數與結合代數的接近程度的是阿廷定理：一個代數A是交錯代數，當且僅當其中任意兩個元素生成的子代數是結合代數。

所謂冪結合代數，是指一代數中任意元素生成的子代數都是結合代數。可以證明，以上提到的各種類型代數都是冪結合代數。在非結合代數中進行計算時，某些恆等式具有很重要的作用。在交錯代數中有常用的毛凡恆等式:；在若爾當代數中有常用的恆等式: ，其中，而運算元 這裡的第二個恆等式，常稱為麥克唐納恆等式。

非結合代數理論在很大程度上是沿著結合環與結合代數的發展道路發展的。結合環與結合代數的發展初期，大致可分為三個階段：有限維代數的韋德伯恩理論，對右理想適合極小條件的環的阿廷理論，以雅各布森根和本原環理論為中心的一般環理論。目前，各種非結合代數都有著不同的發展深度，有些還處於一種相當於結合代數的韋德波恩理論的階段，例如馬爾采夫代數，而交錯代數和若爾當代數的發展最快，大致完成了上述結合環的三個階段。以下是關於交錯代數和若爾當代數的一些結果的簡介。

推廣的弗羅貝尼烏斯定理：實數域上有限維交錯可除代數只有實數域、複數域、四元數代數以及凱萊代數等四種。它們在實數域上的維數是 1,2,4,8。與此定理有關的一個有趣問題是：在實數域中,n個平方數的和乘以n個平方數的和，仍是n個平方數的和嗎？利用這個定理中的四種代數以及其中的共軛元素概念，不難作出當時確是成立的結論。A. 胡爾維茨以及阿爾貝特指出，n只能是1,2,4,8，從而完滿地解決了這個問題。

R.博特、J.W.米爾諾和M.克拉爾應用代數拓撲工具，證明了一個重要的定理：實數域上有限維(非結合)可除代數的維數，只能是1,2,4,8。

阿爾貝特、R.D.謝弗、A.J.佩尼羅和M.佐恩等人證明了與有限維結合代數的韋德伯恩定理相平行的關於交錯代數和若爾當代數的定理。

單代數的分類是有限維代數研究中的一個重要問題。設A是域F上有限維單代數，而且是交錯代數或若爾當代數，此時A必有單位元1,定義之間的乘法適合結合律，凬是A的中心。可以證明，C必是一個域。如果,那麼A稱為F上中心單代數。交錯單代數的品種不多，域F上有限維中心單代數，或是結合代數，或是F上凱萊-迪克森代數。任意域F上的凱萊-迪克森代數是F上8維代數，其定義與實數域上凱萊代數的定義類似，它是實數域上凱萊代數的推廣，其中也有共軛元素的概念。E.克萊因菲爾德把上述結果推廣到任意交錯環上。

中心單若爾當代數的類型則較多，有A、B、C、D、K型。僅僅就例外單若爾當代數(K型單代數)而論，它和五個例外單李代數類型處於類似的地位。取D為域F上的一個凱萊－迪克森代數,D3表D上三階矩陣組成的代數，任取，令 即將矩陣X轉置，並把每一係數換成其共軛元素。可知映射是F上代數D3的一個對合。令 即H(D3)是D3中關於對合的所有埃爾米特元素的全體。可以證明，H(D3)關於若爾當乘法 作成一個若爾當代數。注意到D是F上 8維交錯代數，還可以證明是F上中心單代數，其維數是27，並且是例外若爾當代數。例外單李代數與凱萊－迪克森代數也有密切關係。所謂例外的若爾當代數，即指不是特殊的若爾當代數。若A是結合代數，則A _是李代數，A+是若爾當代數。A_(A+)、A_(A+)的子代數以及與之同構者，稱為特殊李代數（特殊若爾當代數）。雖然不是每一個李環都是特殊的，但是著名的伯克霍夫－維特定理指出，域上李代數都是特殊的。Α.И.希爾紹夫的定理又指出，任意具有兩個生成元的若爾當代數（環）是特殊的。

K.A.日弗拉科夫完整地刻畫了阿廷交錯環。由於缺乏適當的“單側理想”概念，長期未能定出與阿廷結合環相平行的阿廷－若爾當環的概念。 D.M.托平引入二次理想概念：如果對若爾當環 A的子環 B的任意元素 b有AU(b)吇B,那麼B 稱為二次理想。N.雅各布森刻畫了對二次理想有極小條件的若爾當環，與結合環中的阿廷理論相平行。利用運算元U可定義二次若爾當代數,K.麥克里芒作了許多貢獻。結合環的雅各布森根和萊維茨基根等在若爾當環和交錯環中，都有相應的討論。對交錯代數和若爾當代數都有表示論的研究。交錯環與若爾當環和投射平面有聯繫。若爾當代數不僅與李代數、代數群有著聯繫，而且對實分析和複分析都有應用。