在空間,通過一定點且與定曲線相交的一族直線所產生的曲面叫做錐面,這些直線都叫做錐面的母線,那個定點叫做錐面的頂點,定曲線叫做錐面的準線。
給定一條空間曲線C和不在C上的一點O,當點M沿曲線C運動時,連接點O和M的直線OM形成的曲面∑稱為錐面,稱點O為錐面的頂點,曲線C為錐面的準線,直線OM為錐面的母線。
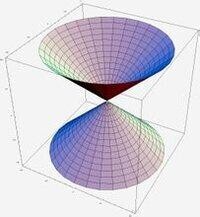
錐面
conical surface動直線經過一定點且保持與定曲線相交所產生的曲面。定點稱為錐面的頂點;定曲線稱為錐面的準線;動直線稱為錐面的直母線。當準線是圓時所得錐面稱為
圓錐面,特別地,如果頂點在過圓心且與圓所在平面垂直的直線上,所得錐面稱為直圓錐面(或正圓錐面)。
直圓錐面也可以看成是過定直線g上一定點O且與該定直線保持定角a(銳角)的動直線產生的,定點O是它的頂點,定直線g是它的軸,定銳角a是它的半頂角。一般地,以平面上的
橢圓、
雙曲線和
拋物線為準線,平面外一點為頂點的錐面,稱為二次錐面,它的標準方程為一般地,在
空間直角坐標系中,關於x,y,z的二次
齊次方程總表示一個以原點為頂點的二次錐面。
橢圓錐面的方程是特別地,當時,它為圓錐面。即在Oxz平面上的直線
繞z軸旋轉而得到。
橢圓錐面與平行於Oxy軸的平面的交線是橢圓與Oxy平面交於原點O。

