S型曲線
費爾許爾斯特提出的分析方法
S型曲線(S-Curve)多存在於分類評定模型(Logit model),邏輯回歸(Logistic regression)模型,屬於多重變數分析範疇,是社會學、生物統計學、臨床、數量心理學、市場營銷等統計實證分析的常用方法。
九紀末,社塔( )觀察,思採納率遵循型曲線。,塔《模仿律》》(《 》)著影響研究傳統,即擴散論社習論。,塔際提濟增型曲線。
塔,模擬基社系。切社程非互。復某,模擬。社模擬傳播、交流觀念。

S型曲線
塔爾德把社會規律還原為支配、模擬的規律,社會互動還原為個人間的心理聯繫,認為社會學即是研究這種心理聯繫的“精神間的心理學”。這種思路應該追溯到S型曲線控制法(邏輯斯諦曲線)及其早期的應用。
費爾許爾斯特—珀爾方程(1833)
1833年,費爾許爾斯特以其著名的邏輯斯諦曲線描述人口增長速度與人口密度的關係,把數學分析方法引入生態學。
歷史上,當孟德爾提出其著名的遺傳定律時,也曾遇到過無法解釋的尷尬:按照他的理論,通過簡單數學計算將得出,某一生物群體中的表現型比例將會逐漸呈現一邊倒的現象。就在這一理論遭到質疑的時候,數學家哈代等人建立起了數學模型,對其定律進行了修正與論證,得到了“遺傳不會影響基因頻率”的正確結論。
數學不僅拯救了生物學支柱之一的孟德爾定律,科學家還通過它得到了費爾許爾斯特—珀爾方程和洛特卡—沃爾泰拉方程。費爾許爾斯特—珀爾方程描述生物種群增長的規律,可以幫助人們計算出人口增長速度與人口密度的關係;而洛特卡- 沃爾泰拉方程則幫助人們認識到農藥的濫用在毒殺害蟲
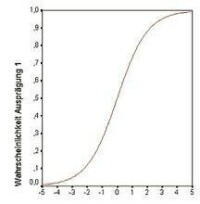
S型曲線
馬爾薩斯於1798年發表的《人口論》一書造成了廣泛的影響。費爾許爾斯特1833年以其著名的邏輯斯諦曲線描述人口增長速度與人口密度的關係。
S型曲線控制法(邏輯斯諦方程)
S型曲線控制法邏輯斯諦方程,即常微分方程:dN/dt=rN(K-N)/K.
字母含義
式中N為種群個體總數,t為時間,r為種群增長潛力指數,K為環境最大容納量。
當一個物種遷入到一個新生態系統中后,其數量會發生變化。假設該物種的起始數量小於環境的最大容納量,則數量會增長。增長方式有以下兩種:
(1) J型增長若該物種在此生態系統中無天敵,且食物 空間等資源充足(理想環境),則增長函數為N(t)=n(p^t).其中,N(t)為第t年的種群數量,t為時間,p為每年的增長率(大於1).圖象形似J形。
(2) S型增長若該物種在此生態系統中有天敵,食物 空間等資源也不充足(非理想環境),則增長函數滿足邏輯斯諦方程。圖象形似S形.
工程S曲線(S-Curve)
即按照對應時間點給出的累計的成本、工時或其他數值的圖形。該名稱來自曲線的形狀如英文字母S(起點和終點處平緩,中間陡峭),項目開始時緩慢,中期加快,收尾平緩的情況造成這種曲線。
邏輯回歸模型(Logistic回歸模型)
通常人們將“Logistic回歸”、“Logistic模型”、“Logistic回歸模型”及“Logit模型”的稱謂相互通用,來指同一個模型,唯一的區別是形式有所不同:logistic回歸是直接估計概率,而logit模型對概率做了Logit轉換。不過,SPSS軟體好像將以分類自變數構成的模型稱為Logit模型,而將既有分類自變數又有連續自變數的模型稱為Logistic回歸模型。至於是二元還是多元,關鍵是看因變數類別的多少,多元是二元的擴展。
城市化進程的倒S型曲線(1975)
1975年,美國城市學者諾瑟姆Ray.M.Northam發現並提出了“諾瑟姆曲線”,這個曲線表明:發達國家的城市化大體上都經歷了類似正弦波曲線上升的過程。
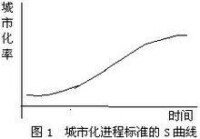
城市化進程呈現一條被拉平的倒S型曲線,當城市化超過30%時,進入了快速提升階段。城市化的發展在時間和空間兩個維度展開,表現為階段性和地區差異。
諾瑟姆在總結歐美城市化發展歷程的基礎上,把城市化的軌跡概括為拉長的S型曲線。他把城市化進程分為三個階段:第一是城市化起步階段,城市化水平較低,發展速度也較慢,農業佔據主導地位;第二是城市化加速階段,人口向城市迅速聚集,城市化推進很快。隨著人口和產業向城市集中,市區出現了勞動力過剩、交通擁擠、住房緊張、環境惡化等問題。小汽車普及后,許多人和企業開始遷往郊區,出現了郊區城市化現象;第三是城市化成熟階段,城市化水平比較高,城市人口比重的增長趨緩甚至停滯。在有些地區,城市化地域不斷向農村推進,一些大城市的人口和工商業遷往離城市更遠的農村和小城鎮,使整個大城市人口減少,出現逆城市化現象。
S型曲線
長期以來,正統經濟學一直以“理性人”為理論基礎,通過一個個精密的數學模型構築起完美的理論體系。而卡尼曼教授等人的行為經濟學研究則從實證出發,從人自身的心理特質、行為特徵出發,去揭示影響選擇行為的非理性心理因素,其矛頭直指正統經濟學的邏輯基礎——理性人假定。

S型曲線
而1947年Herbert Simon(1978年榮獲諾貝爾經濟學獎)考慮到人的心理因素在經濟行為中的作用,提出“有限理性”理論。他認為,在當今的複雜社會裡,一個人不可能獲得所有必要的信息來做出合理的決定。

S型曲線
查爾斯·漢迪新變革的“S型曲線”
查爾斯·漢迪(Charles Handy)的《空雨衣》(又譯為《覺醒的年代》)在《覺醒的年代》提出了三種管理思想架構:一是在持續成長的同時施行新變革的“S型曲線”,二是必須在做與做得到之間取得平衡的“甜甜圈原理”,三是充分運用雙贏藝術的“中國式契約”。
查爾斯·漢迪組合式人生
在組合式人生的時間分配上,他及妻子伊麗沙白每年分配150天用於純粹的創造性工作,寫作和攝影以及相關的閱讀與研究,100天用於商業和管理活動,基本是到國外做巡迴演講,再拿30天時間用於各種志願性工作,除此之外還有85天自由時間,可用於每周的休息和應對突發事件,這種安排很好地實現了生活的平衡。
漢迪對政治和社會的興趣跟管理一樣大,屬通識型學者。他晚年的著述是糅合了市場經濟、企業文化與人道觀點,低聲地在提倡營利,大聲地在鼓吹對人的尊重。近年來他一直在探討:什麼樣的工作方式與生活方式是最適合21世紀的社會?漢迪在西方社會一生的體驗使他相信:個人的自由與獨立,要與財富的分享、社會的正義相互平衡。漢迪不僅是管理大師,更是人道主義者。
在Photoshop中,一般指用曲線調整時候, S形是提高對比度.,反s形正好相反。
S函數是System Function的簡稱。在很多情況下,Simulink現有的模塊已經不能滿足用戶的需要,這時可以自己編寫相應的代碼來完成對模塊功能的需求。S函數則提供了一個代碼和Simulink模塊之間的介面,用來實現對模塊的編程。其中S函數的代碼可以用Matlab語言編寫,也可以是C、C++、Ada、Fortran等語言編寫。