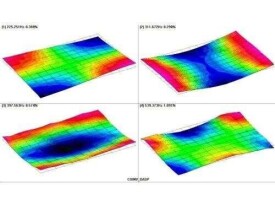
模態質量

歸一化主要是為了簡化計算，常用的方式就是將每個自由度的主陣型第一個元素變為1。模態質量應該是前乘陣型矩陣的轉置，后乘陣型矩陣得到的對角質量矩陣，還有一種歸一化方法就是將這個對角質量陣變成單位陣。

模態質量有意義，反映了體系中有多少質量對這階模態振型有大的影響，每一階是不同的。歸一化振型就是計算的振型（計算位移值）除以最大的值，變成最大值為1，反映體系各處相對變形。廣義質量矩陣不是模態質量。模態質量計算還涉及到振型和振型參與係數。

振型參與係數：每個質點質量與其在某一振型中相應坐標乘積之和與該振型的主質量（或者說該模態質量）之比，即為該振型的振型參與係數。一階振型自振頻率最小(周期最長),二階，三階。振型的自振頻率逐漸增大. 地震力大小和地面加速度大小成正比，周期越長加速度越小，地震力也越小。自振振型曲線是在結構某一階特徵周期下算得的各個質點相對位移(模態向量)的圖形示意。在形狀上如實反映實際結構在該周期下的振動形態。振型零點是指在該振型下結構的位移反應為0。振型越高，周期越短，地震力越大，但由於我們地震反應是各振型的迭代，高振型的振型參與係數小。特別是對規則的建築物，由於高振型的參與係數小，一般忽略高振型的影響。

也就是一個系統的振動雖然非常複雜，各種耦合，但是其實只是是一些獨立的諧振子的疊加罷了。

這些諧振子按照個子不同的頻率做簡諧運動，簡單的不能再簡單。但是混合在一起表現的就非常複雜，讓我們好像覺得這是個複雜系統。

所以分析這個系統最好的方法，就是把這些諧振子找出來。這叫做解耦，把本來耦合的系統分解成獨立的。而這些諧振子，我們叫他們模態。

比如一根兩端固定的梁，他要怎麼振動我們完全不知道，它有無窮個質點，也就有無窮個自由度，我們只知道這些自由度是怎麼互相牽連罷了（彈性力學方程）。但是解耦后我們發現其實只是這幾個簡單的振動形式疊加而已（所以模態也叫作振形）。這些振形隨時間按照自己的固有頻率振動，除了形狀比較奇怪以外（比如變速箱殼的模態分析，會有看起來非常扭曲的那種振形），和高中學的小塊彈簧簡諧振動沒區別，能輕鬆的解決。

至於使用方法，一般是振動力學的模態疊加法。這個方法在有限元中被也用來解決非衝擊的的動力學問題。

子空間法比較適合於提取類似中型到大型模型的較少的振型。

1、需要相對較少的內存；

2、實體單元和殼單元應當具有較好的單元形狀，要對任何關於單元形狀的警告信息予以注意；

3、在具有剛體振型時可能會出現收斂問題；

4、建議在具有約束方程時不要用此方法。

如果模型中的集中質量不會引起局部振動，例如象梁和桿那樣，可以使用縮減法：

1、它是所有方法中最快的；

2、需要較少的內存和硬碟空間；

3、使用矩陣縮減法，即選擇一組主自由度來減小剛度矩陣和質量矩陣的大小；

4、縮減的剛度矩陣是精確的，但縮減的質量矩陣是近似的，近似程度取決於主自由度的數目和位置；

5、在結構抵抗彎曲能力較弱時不推薦使用此方法，如細長的梁和薄殼。

在模態分析中一般忽略阻尼，但如果阻尼的效果比較明顯，就要使用阻尼法：

1、主要用於迴轉體動力學中，這時陀螺阻尼應是主要的；

2、在 ANSYS 的 BEAM4 和 PIPE16單元中，可以通過定義實常數中的 SPIN（旋轉速度，弧度/秒）選項來說明陀螺效應；

3、計算以複數表示的特徵值和特徵向量。