介值定理
區間函數值介於大小值之間
介值定理,又名中間值定理,是閉區間上連續函數的性質之一,閉區間連續函數的重要性質之一。在數學分析中,介值定理表明,如果定義域為[a,b]的連續函數f,那麼在區間內的某個點,它可以在f(a)和f(b)之間取任何值,也就是說,介值定理是在連續函數的一個區間內的函數值肯定介於最大值和最小值之間。
如果一個連續函數在區間內有相反符號的值,那麼它在該區間內有根存在(博爾扎諾定理)。
設函數y=f(x)在閉區間[a,b]上連續,且在這區間端點處取值不同時,即:f(a)=A,f(b)=B,且A≠B。那麼,不論C是A與B之間的怎樣一個數,在閉區間[a,b]內至少有一點ξ,使得f(ξ)=C。
特別地,如果f(a)與f(b)異號,那麼在開區間(a,b)內至少有一點ξ,使得f(ξ)=0(a<ξ>
在[a,b]上連續的曲線與。
特別地,如果A與B異號,則連續曲線與x軸至少相交一次。
“介值定理”是閉區間上連續函數的性質之一。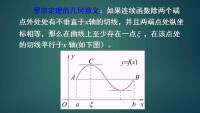

介值定理
該定理可以根據實數的完整性來證明:
我們將證明第一種情況, ,第二種情況類似。
讓S是[a,b]中的所有x的集合,讓 。S是非空的因為a是S的元素,並且b是S的邊界。因此,通過完整性,存在上限 。也就是說,c是大於或等於S的每個元素的最小數。我們稱 。
存在 。由於f是連續的,當 時,存在 ,使得 。這意味著
對於所有的 ,存在屬於S的 ,使得
選擇 ,這顯然不會包含在S中,所以我們有
兩種不等式
對於所有的 都是成立的,如我們所說,我們推導出 是唯一可能的值。
介值定理也可以使用非標準分析的方法來證明,這在非常嚴格的基礎上提出了涉及無限小數的“直觀”論證。(見文章:非標微積分)
對於上面的u=0,該聲明也稱為博爾扎諾定理。這個定理在1817年被伯納德·博爾扎諾(BernardBolzano)首次證明。奧古斯丁-路易·柯西在1821年提供了一個證據。兩者的靈感來自於對約瑟夫·路易斯拉格朗日函數的分析正式化的目標。連續函數具有中間值的想法早有起源。西蒙·斯蒂文通過提供用於構造解的十進位擴展的演演算法,證明了多項式的介值定理(以立方為例)。該演演算法迭代地將間隔細分為10個部分,在迭代的每個步驟產生一個附加的十進位數字。在給出連續性的正式定義之前,將介值作為連續函數定義的一部分。支持者包括路易斯·阿博加斯特(LouisArbogast),沒有跳躍的函數滿足介值定理,並且具有尺寸對應於變數大小的增量。早期的作者認為結果是直觀的,不需要證明。博爾扎諾和柯西的觀點是定義一個連貫性的概念(就柯西案中的無限小數而言,在博爾扎諾案中使用實際的不平等),並提供基於這種定義的證據。
“Darboux函數”是具有“介值屬性”的實值函數f,即滿足介值定理的結論:對於f的域中的任何兩個值a和b,以及任何y在f(a)和f(b)中,a和b之間有一些c,f(c)=y。介值定理說每個連續函數都是一個Darboux函數。但是,並不是每個Darboux功能都是連續的;即介值定理的相反是錯的。
例如,對於x>0和f(0)=0,取 定義的函數 在x=0時連續,這個函數在x=0處不連續,但是該函數具有介值屬性。
歷史上,這個介值屬性被建議為實數函數連續性的定義,但這個定義沒有被採納。
Darboux定理指出,由某些區間上某些其他函數的區分產生的所有函數都具有介值屬性(儘管它們不需要連續)。
定理意味著,在世界各地的任何一個大環境中,對於溫度,壓力,高程,二氧化碳濃度來說,如果是連續變化的,那麼總是會存在兩個與該變數相同值的對映點。
證明:將f作為圓上的任何連續函數。在圓的中心繪製一條線,在兩個相對的點A和B處與其相交。令d由差定義。如果線旋轉180度,將取代值-d。由於介值定理,必須有一些中間旋轉角,其中d=0,因此 在該角度。
對於任何封閉的凸n(n>1)尺寸形狀。具體來說,對於其領域是給定形狀的任何連續函數,以及形狀(不一定是其中心)內的任何點,相對於函數值相同的給定點存在兩個對象點。證明與上述相同。
這個定理也是為什麼旋轉搖擺表將使其變得穩定的解釋(受到某些容易遇到的限制)。
特殊情況
如果f(a)與f(b)異號,那麼在開區間(a,b)內至少有一點ξ,使得f(ξ)=0(a<ξ零點定理。
幾何意義
連續曲線弧y=f(x)與水平直線y=C至少相交於一點。特別地,如果A與B異號,則連續曲線與x軸至少相交一次。
在閉區間[a,b]上連續的函數f(x)的值域為閉區間[m,M],其中m與M依次為f(x)在[a,b]上的最小值和最大值。
