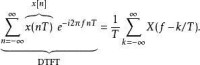降採樣
降採樣
在數位信號處理領域中,降採樣,又作減採集,是一種多速率數字信號處理的技術或是降低信號採樣率的過程,通常用於降低數據傳輸速率或者數據大小。跟插值互補,插值是用來增加取樣頻率。降採樣的過程中會運用濾波器降低混疊造成的失真,因為降採樣會有混疊的情形發生,系統中具有降採樣功能的部分稱為降頻器。
降採樣因子(常用表示符號為"M")一般是大於1的整數或有理數。這個因子表達採樣周期變成原來的M倍,或者等價表示採樣率變成原來的1/M倍。採樣率的降低會造成頻譜的壓縮,因此需要利用濾波器確保在較低的採樣頻率下不發生混疊,確保奈奎式採樣定理依舊成立。
降採樣整數M倍的過程可以被分解成兩個部分:
利用數位低通濾波器去除訊號中的高頻成分防止混疊。
對過濾高頻后的訊號降採樣M倍,換言之,保留原訊號中間隔為M的取樣點
1.
利用數位低通濾波器去除訊號中的高頻成分防止混疊。
2.
對過濾高頻后的訊號降採樣M倍,換言之,保留原訊號中間隔為M的取樣點
若僅少了第一個步驟,訊號的高頻成分會在降低採樣速率的過程中被混入低頻訊號中,這樣的失真效應我們稱為混疊,因此第一個步驟是為了降低混疊影響至可以接受的程度,降採樣中的濾波器稱為 反混疊濾波器,下面討論如何設計反混疊濾波器。
若用無限脈衝響應的方法設計反混疊濾波器,則濾波的過程需要在降低採樣速率前從輸出端回傳資訊到輸入端,若用有限脈衝響應的方法設計反混疊濾波器,濾波的過程較為簡單因為我們只需要考慮間隔為M的採樣點,濾波的過程表示成:
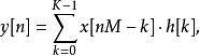
降採樣
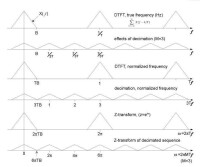
圖一
序列h[·]是數位濾波器的脈衝響應、K是它的長度,序列x[·]為要被降採樣的原始訊號的取樣點,一般來說在算出y[n]後計算y[n+1]最簡單的方法是讓x[·]的索引增加M然後重新計算卷積,在大部分的情況下M=2,h[·]可以被設計成半頻帶濾波器,序列h[k]中將近一半的係數為0,因此卷積的計算過程會被大大簡化。
每隔M個取樣點取樣脈衝響應的係數成為一個次序列,總共有M個降採樣的脈衝響應次序列,內積的結果是每個次序列.跟對應的取樣點x[·] 內積的總和。此外,由於採樣周期變成M倍,每個降採樣后的次序列會獨立在每個內積中,數列x[·] 的採樣點只會出一組內積之中而不會出在其他組的內積里,因此可以用M組有限長度頻率響應數位濾波器同時多工地算出M組內積,M組輸出值最後平行加總。這個觀點提供不同的硬體實作方法,很可能適合多處理器的架構。換句話說,輸入的串流經過分工並送去M組濾波器並將輸出加總,上述的架構稱為多項位濾波器。
圖一: 3種不同的常見頻率單位下的降採樣頻譜效應比較。
反混疊濾波器
降採樣
最上面那組圖片的上面那張圖的橫軸代表離散時間傅立葉轉換,也就是X(f)的傅立葉級數表示方式:
降採樣
降採樣
降採樣
中間那組圖頻率f的單位改為標準化頻率,這時周期為1而0.5的位置對應到奈奎氏取樣頻率,一般反混疊濾波器的設計會以圖形的頻率單位為標準,因此截止頻率也要改由以標準化頻率作為單位,此時截止頻率 被標準化為 這個值的單位為(秒/取樣)*(周期數/秒)=周期數/取樣。
降採樣
降採樣
降採樣
令 M/L代表降採樣因子,M,L都是整數,M>L,分數倍降採樣可以被分解成兩個步驟
以L倍頻率升採樣
以1/M倍頻率降採樣
1.
以L倍頻率升採樣
2.
以1/M倍頻率降採樣
降採樣
bit/樣本) × 2 (聲道))降低至705,600位元秒。