三角函數對數表
三角函數對數表
三角函數對數表是一種常用的數據表,指具有一定間隔的銳角三角函數值的常用對數值表。如正弦對數表、餘弦對數表、正切對數表、餘切對數表,常見有4位、5位(中學生用)和6—10位(工程和科研用)的三角函數對數表。由於正弦函數與餘弦函數,正切函數與餘切函數在[0°,90°]內互余,所以造表時常把正弦對數和餘弦對數造入同一表中,把正切對數和餘切對數造入同一表中,因此,查正弦函數和正切函數的對數時,從表的左邊自上往下查尋;查餘弦函數和餘切函數的對數時,從表的右邊自下往上查尋。岡特(E.Gunter)曾在1620年發表的《三角法則》中給出第一張相隔1′的七位數正弦對數和正切對數表,並引入餘弦和餘切概念。
求已知角的三角函數的對數,可以先由三角函數表求得這個巳知角的三角函數,再由對數表求所得結果的對數,例如:求。可先由三角函數表求得:;再由對數表求得 ;因此得到。
按照上面的方法需要進行兩次查表,這是較麻煩的,如果利用三角函數對數表,就可以直接查得已知角的三角函數的對數。
解直角三角形或斜三角形時,除了利用三角函數表來進行計算外,也可利用對數原理和“四位數學用表”中的三角函數對數表來進行計算。三角函數對數表,給出的不是三角函數的數值,而是這些數值的常用對數,這些常用對數不但包含了三角函數對數的尾數,而且包含了它們的首數,由於當真數增加時,它的常用對數也隨著增加,又因為當角由0增加到 時,角的正弦、正切的值隨著增加,而餘弦、餘切的值隨著減少,所以當角由0增加到 時,角的正弦、正切的常用對數隨著增加,而餘弦、餘切的常用對數卻隨著減少。另外,由於大於1的數的常用對數是正的,小於1的數的常用對數是負的,根據三角函數的值域可知,正弦、餘弦的常用對數的首數是負數或零;正切的常用對數的首數,當角在區間 是負數,當角在區間 內是正數,餘切的常用對數的首數的正負和正切相反。三角函數對數表的結構與使用方法和三角函數表相類似。
三角函數對數表所給出的對數尾數部分是具有四個有效數字,就是說,當角度是精確數時,由表查得的三角函數對數,其絕對誤差界不超過0.0005,如果角度是近似數,則由表查得的三角函數對數,其尾數部分不一定全部是有效數字,在一般情況下可按下述法則處理:
當角準確到0.5',5' 和30'時,它的三角函數對數值的尾數可分別保留四位、三位和二位數字。即查表后結果都要化整到上述可保留的數位。當三角函數對數的尾數有四位、三位和二位有效數字時,它的對應角度可分別保留分數的個位數字、分數的十位數字和度數的個位數字。查表時,可將已知三角函數對數值多保留一位後備數字,但查表后結果應化整到上述可保留的數位。
例1 求.
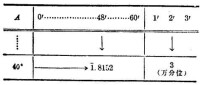
三角函數對數表
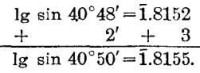
三角函數對數表
例2 求.
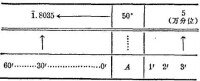
三角函數對數表
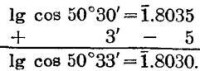
三角函數對數表
