莫爾斯理論

微分拓撲學中利用微分流形上僅具非退化臨界點的實值可微函數(稱為莫爾斯函數)研究所給流形性質的分支。它是H.M.莫爾斯在20世紀30年代創立的。由莫爾斯理論得知，微分流形與其上的光滑函數緊密相關，利用光滑函數不僅能研究微分流形的局部性質，而且某些光滑函數例如莫爾斯函數包含了刻劃流形整體性質的豐富信息。莫爾斯理論主要分兩部分，一是臨界點理論，一是它在大範圍變分問題上的應用。

確切地說，假設ƒ是n維微分流形M上的實值可微函數，ƒ的臨界點p是指梯度向量場gradƒ的零點，即在局部坐標下使得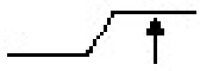的點。ƒ的全部臨界點的性態與流形M本身的拓撲結構有密切的關係，探索這些關係就是臨界點理論的主要任務。例如，著名的莫爾斯不等式就是這樣一種關係：

，

……

……

，

式中Rk是n維閉流形M的k維模2貝蒂數，即同調群的秩,是M上非退化函數ƒ的指數為k的臨界點的個數。這裡說ƒ是非退化函數，是指ƒ的任何臨界點p均非退化，即在局部坐標下ƒ在p處的黑塞矩陣之秩為n；這個矩陣的負特徵值的個數稱為臨界點p的指數。莫爾斯不等式是H.M.莫爾斯本人在20世紀20年代建立的基本結果，後來有了遠為一般的結果。例如，考慮圖1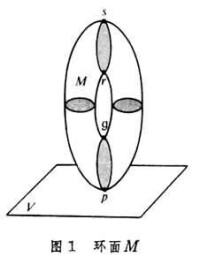中環面M 關於水平切面V的高度函數，其中p,q,r,s是ƒ的四個非退化臨界點，其指數分別為0,1,1,2,因為可以適當選擇局部坐標，使得在p的鄰近 (旋轉拋物面),在q的鄰近 (鞍面)，在r的鄰近 （鞍面）,在s的鄰近 (旋轉拋物面)。命不難看出，當α由小變大經過各個臨界值時,Mα 的同倫型發生表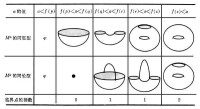中所列的變化。

可見，當α從小變大經過指數為λ的臨界點時,Mα 的同倫型變化相當於粘上一個λ維胞腔，從而整個環面M的同倫型相當於由一個 0維胞腔、兩個一維胞腔以及一個二維胞腔組成的CW復形，這樣就把M的同倫型與ƒ 的臨界點的性態聯繫起來了。如果把這個事實推廣到一般情形就是：

臨界點理論的基本定理 命M是微分流形,是非退化函數，並且任何Mα 都是緊緻集。於是，每個Mα 都具有一個有限CW復形的同倫型，從而整個M具有一個至多是可數的CW復形的同倫型：對於指數為λ的每個臨界點，這個復形有一個λ維胞腔。

臨界點理論的應用中最完美的是對測地線問題的應用，這就是變分學的莫爾斯理論。例如，考慮完備黎曼流形M上兩個固定端點p和q之間的測地線問題，即是使弧長為極小的變分問題：

式中 表示M上的逐段光滑道路，這個變分問題的泛極線就是所謂測地線。於是，從p 到q 的所有光滑測地線的性態與流形M的拓撲結構之間是否有什麼關係，這就是大範圍變分學要研究的主要問題，可以應用臨界點理論的框架得到相似的結果。命表示M上從p到q所有逐段光滑道路組成的空間，具有尺度拓撲。式中ρ 表示M上由黎曼尺度導出的距離函數；表示ω 上的弧長。

大範圍變分學基本定理 命M是完備黎曼流形，沿任何測地線不共軛，則具有可數CW復形的同倫型：對於從p到q每條指數為λ的測地線，這個復形有一個λ維胞腔。

隨著拓撲學的發展，莫爾斯理論本身也有很大的飛躍。例如，由於臨界點定義為梯度向量場gradƒ 的零點，自然可以考慮n維閉流形M上一般向量場X 的零點與M的拓撲結構之間的關係，即M上的動力系統：

的奇點與M的拓撲結構的關係。S.斯梅爾在某些假設下得到了形式相同的莫爾斯不等式，不過這時αk表示向量場X 的k型零點的個數,bk表示k型閉軌線的條數。斯梅爾正是在這個基礎上完成了他關於高維龐加萊猜想的卓越工作，這是微分拓撲學的重大成就之一。其次，由於測地線問題是一維變分問題，本來是無限維的空間Ω才能化為有限維流形應用臨界點理論來處理。但一般的多維變分問題就無法做到這一點，因而要求發展無限維流形上的臨界點理論，直接處理相應的無限維空間Ω，從而把原來的兩個方面統一起來。