同倫
同倫
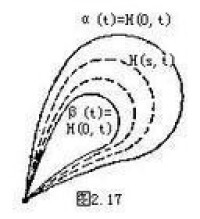
同倫
如果存在連續映射f:X→Y和g:Y→X,使得g·f與恆同映射idx:X→X同倫,f·g與恆同映射idy:Y→Y同倫,則稱X與Y同倫等價。稱f和g是同倫等價映射,g是f的一個同倫逆。
在同倫變換下保持不變的性質,就稱為同倫不變數。比如虧格(洞眼的個數),歐拉示性數等等。但是維數就不是同倫不變數。
這是因為兩者是同倫的,即麵包圈可以連續形變成咖啡杯。
在施瓦辛格主演的科幻電影《終結者2》裡面那個液態機器人殺手,它的每次變化都可以視為同倫變換。但那次被施瓦性格用槍打爆腦袋不能算同倫變化,因為這不是連續地形變。
同倫是關於映射的等價關係,同倫等價才是關於空間的等價關係。最後舉的兩個例子更適合在同胚的概念中提及,在此處提雖然從邏輯上講沒錯,但也容易讓初學者混淆。建議舉不同倫的例子如下:兩個映射,一個是圓周到自身的恆同映射,另一個則是自變數在圓周上轉一圈時相應的映射的值在圓周上轉兩圈。舉同倫等價的例子如下:“日”字和“8”字。
同倫和倫移的定義由brouwer於1911年給出,雖然它的直觀的觀念形變(deformation)早在lagrange時代的變分學中已經出現並被使用,或許還可以追溯到更早。