單位圓
數學術語之一
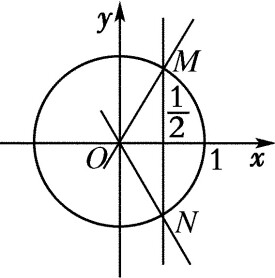
單位圓指的是平面直角坐標繫上,圓心為原點,半徑為單位長度的圓。
如果單位圓上的點位於第一象限,那麼x與y是斜邊長度為1的直角三角形的兩條邊,根據勾股定理,x與y滿足方程:
單位圓
在三角學中,單位圓通常是指歐幾里德平面直角坐標系中圓心為、半徑為 1 的圓。在教科書中,它常常出現在三角函數入門的那幾頁,並且與稱為三角函數線的幾條線段在一起,用於定義或解釋實數的三角函數值。一般地,在複平面內,n 個 n 次的單位根所對應的點正。
1. 在複平面(即高斯平面)上,單位圓誘導了著名的歐拉公式和棣莫佛定理。換句話說,單位圓上的點表示模長為1的複數,它誘導了複數的三角形式和指數形式之間的關係。
2. 單位圓上有自然的群結構:即弧度的加法群結構。換句話說,就是模長為1的複數集合 上有一個自然的乘法結構。
3. 單位圓誘導了幾何反演變換,這和複變函數論的諸多結論密切相關。
4. 單位圓是最簡單的非單連通 的拓撲空間之一,常記為. 它的基本群同構於整數群。
5. 單位圓同胚於射影直線,是拓撲學中最基本的研究對象。這個同胚映射來自於從北極點作的球極投影。
6. 單位圓盤到自身的連續映射一定存在不動點。這就是著名的布威勞爾 不動點定理。
1. 單位圓廣泛應用於三角函數,對正弦函數,餘弦函數,正切函數等的定義,函數圖像的繪製有重要作用!
2. 定義三角函數線
3. 單位圓應用於檢測心率異常與否的一種圖像標準。