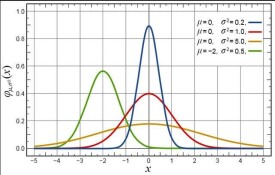
高斯濾波
信號的濾波器
高斯濾波是一種線性平滑濾波,適用於消除高斯雜訊,廣泛應用於圖像處理的減噪過程。通俗的講,高斯濾波就是對整幅圖像進行加權平均的過程,每一個像素點的值,都由其本身和鄰域內的其他像素值經過加權平均后得到。高斯濾波的具體操作是:用一個模板(或稱卷積、掩模)掃描圖像中的每一個像素,用模板確定的鄰域內像素的加權平均灰度值去替代模板中心像素點的值。
實質上是一種信號的濾波器,其用途是信號的平滑處理,數字圖像用於後期應用,其雜訊是最大的問題,由於誤差會累計傳遞等原因,很多圖像處理教材會在很早的時候介紹Gauss濾波器,用於得到信噪比SNR較高的圖像(反應真實信號)。於此相關的有Gauss-Laplace變換,其實就是為了得到較好的圖像邊緣,先對圖像做Gauss平滑濾波,剔除雜訊,然後求二階導矢,用二階導的過零點確定邊緣,在計算時也是頻域乘積=>空域卷積。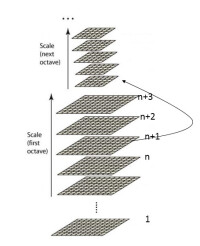

高斯濾波
可以簡單地理解為,高斯濾波去噪就是對整幅圖像像素值進行加權平均,針對每一個像素點的值,都由其本身值和鄰域內的其他像素值經過加權平均后得到。
高斯濾波的具體操作是:用一個用戶指定的模板(或稱卷積、掩膜)去掃描圖像中的每一個像素,用模板確定的鄰域內像素的加權平均灰度值去替代模板中心像素點的值。
高斯濾波(高斯平滑)是圖像處理,計算機視覺裡面最常見的操作。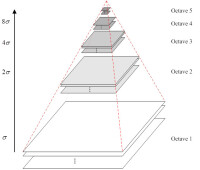

高斯濾波
在圖像處理中,高斯濾波一般有兩種實現方式,一是用離散化窗口滑窗卷積,另一種通過傅里葉變換。最常見的就是第一種滑窗實現,只有當離散化的窗口非常大,用滑窗計算量非常大(即使用可分離濾波器的實現)的情況下,可能會考慮基於傅里葉變化的實現方法。
由於高斯函數可以寫成可分離的形式,因此可以採用可分離濾波器實現來加速。所謂的可分離濾波器,就是可以把多維的卷積化成多個一維卷積。具體到二維的高斯濾波,就是指先對行做一維卷積,再對列做一維卷積。這樣就可以將計算複雜度從O(M*M*N*N)降到O(2*M*M*N),M,N分別是圖像和濾波器的窗口大小。