共點力平衡

（1）平衡狀態：物體處於靜止或勻速直線運動狀態。

一個物體在共點力的作用下，如果保持靜止或者做勻速直線運動，我們就說這個物體處於平衡狀態。

由此可見，平衡狀態分兩種情況：

一種是靜態平衡，此時，物體運動的速度，物體的加速度；

另一種狀態是動態平衡，此時，物體運動的速度，物體的加速度。

（2）物體處於平衡狀態，其受力必須滿足合外力為零，即，.這就是共點力作用下物體的平衡條件。

如果物體在三個共點力作用下處於平衡狀態，那麼這個力的大小分別與另外兩個力的夾角的正弦成正比。

（1）二力平衡：如果物體在兩個共點力的作用下處於平衡狀態，這兩個力必定大小相等、方向相反，為一對反力。

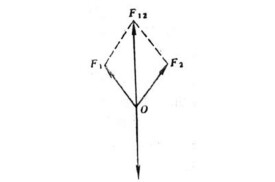
（2）三力平衡：如果物體在三個力的作用下處在平衡狀態，那麼這三個力不是平行的話就必共點，而且其中兩個力的合力必與第三個力大小相等、方向相反。

根據這個特點，我們求解三力平衡問題時，常用的方法是力的合成法，當然也可以用分解法（包括正交分解）、力的矢量三角形法和相似三角形法等。

（3）多力平衡：如果物體受多個力作用處於平衡狀態，其中任何一個力與其餘力的合力大小相等、方向相反。

一個物體在三個共點力作用下處於平衡狀態時，將其中任意一個力沿其他兩個力的反方向分解，這樣把三力平衡問題轉化為兩個方向上的二力平衡問題，則每個方向上的一對力大小相等。

對於三力平衡時，將三個力中的任意兩個力合成為一個力，則其合力與第三個力平衡，把三力平衡轉化為二力平衡問題。

物體受到三個或三個以上力的作用處於平衡狀態時，常用正交分解法列平衡方程求解：。為方便計算，建立坐標系時以使儘可能多的力落在坐標軸上為原則。

若一個系統中涉及兩個或者兩個以上物體的平衡問題，在選取研究對象時，要靈活運用整體法和隔離法。對於多物體問題，如果不求物體間的相互作用力，優先採用整體法，這樣涉及的研究對象少，未知量少，方程少，求解簡便；很多情況下，通常採用整體法和隔離法相結合的方法。

物體受三個共面非平行力作用而平衡時，這三個力必為共點力。

三力平衡時，三力合力為零。三個力可構成一個封閉三角形，如圖9所示。

物體受到三個共點力的作用而處於平衡狀態，畫出其中任意兩個力的合力與第三個力等值反向的平行四邊形中，可能有力三角形與題設圖中的幾何三角形相似，進而得到力的三角形與幾何三角形對應邊成比例，根據比值便可計算出未知力的大小與方向。

1．圖解法 對研究對象進行受力分析，再根據平行四邊形定則或三角形定則畫出不同狀態下力的矢量圖(畫在同一個圖中)，然後根據有向線段(表示力)的長度變化情況判斷各個力的變化情況。 

2．圖解法主要用來解決三力作用下的動態平衡問題 所謂動態平衡問題就是通過控制某一物理量，使物體的狀態發生緩慢變化。從宏觀上看，物體是運動的，但從微觀上理解，物體是平衡的，即任一時刻物體均處於平衡狀態。 

3．利用圖解法解題的條件是 

(1)物體受三個力的作用而處於平衡狀態。

(2)一個力不變，另一個力的方向不變或大小不變，第三個力的大小、方向均變化。