卡瓦列利原理

夾在兩條平行直線之間的兩個平面圖形，被平行於這兩條直線的任意直線所截，如果所得的兩條截線長度相等，那麼，這兩個平面圖形的面積相等。

夾在兩個平行平面之間的兩個立體圖形，被平行於這兩個平面的任意平面所截，如果所得的兩個截面面積相等，那麼，這兩個立體圖形的體積相等。

卡瓦列利將定理中的相互比較的兩個平面或立體圖形稱為“類比圖”（analogues）。他首先證明定理的第一部分，即兩個平面類比圖面積相等。

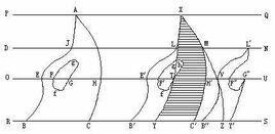
如圖3-1-1所示。設夾在兩平行線PQ、RS之間有兩個平面圖形ABC和XYZ.其中不妨設ABC有一空的部分FfGg。任作兩條平行於PQ、RS的直線DN、OU，DN截兩圖所得的截線分別為JK和LM，JK=LM；OU截ABC得兩條截線段EF和GH,截XYZ得截線段TV，EF+GH=TV。

沿PQ、RS平移圖形ABC，將它疊置於圖形XYZ之上（圖中A與X兩點重合）。如果ABC與XYZ完全重合，那麼顯然它們的面積相等；如果ABC於XYZ不完全重合，那麼ABC的某一部分XLhTYC¢M與XYZ的一部分XLhTYC¢M重合。顯然，ABC的截線EF、GH在ABC平移之後仍在直線OU上，故E¢F¢、TH¢與TV仍在同一直線上。由假設，E¢F¢+TH¢=EF+GH=TV,因此E¢F¢=H¢V.而E¢F¢和H¢V分別在圖形ABC和XYZ和彼此不重合的部分LB¢YTF¢和MC¢Z,Thg（分別稱為ABC和XYZ的剩餘圖形）中。可見，當圖形ABC有一部分不與XYZ重合時，圖形XYZ必剩餘某一部分不與ABC重合。

由於對於ABC的剩餘圖形中的任一平行於PQ,RS的截線段，相應地在XYZ的剩餘圖形中都有一條與之共線的截線段（如果剩餘圖形有若干部分，則截線可能不止一條），因此ABC與XYZ的剩餘圖形必夾在同樣的兩條平行線之間。又因為它們中的對應截線段相等（E¢F¢=H¢V），因此ABC、XYZ的剩餘圖形滿足ABC和XYZ所滿足的條件，他們仍為類比圖。

然後，沿RS平移ABC的剩餘圖形LB¢YTF¢，將它疊置於XYZ的剩餘圖形之上，使其一部分VB¢¢Z與MC¢Z的一部分VB¢¢Z重合。則和前面一樣可證明其中一個有剩餘圖形時，另一個必有剩餘圖形，這些剩餘圖形夾在同樣的兩條平行線之間，並且對應截線段相等。設L¢VZY¢G¢¢F¢¢是LB¢YTF¢的剩餘圖形，而MC¢B¢¢V，Thg為MC¢Z，Thg的剩餘圖形，則他們是夾在DN、RS之間的類比圖。然後再沿RS平移L¢VZY¢G¢¢F¢¢，將它疊置於MC¢B¢¢V和Thg上。不難理解，同樣的步驟可以不斷進行下去，直到整個圖形ABC被疊置完。根據前面的證明，此時XYZ也不再有剩餘圖形了。這樣，ABC於XYZ的部分圖形相繼重合，直到最後所有部分均重合。從而ABC與XYZ面積相等。

若將上述證明中的ABC和XYZ改為立體圖形，截線相應改為截面，則同樣可以證明定理的第二部分，即兩立體類比圖體積相等。

卡瓦列里把平面圖形看作是由平行的等距線段組成的，把立體圖形看作是由彼此平行的、等距離的平面片組成的．這些線段就是平面圖形的不可分量而這些平面片就是立體圖形的不可分量．卡瓦列里的具體方法是先建立兩個給定的幾何圖形的不可分量之間的一一對應關係，並且設法使對應的不可分量具有某種不變的比例，當其中一個圖形的面積或體積已求出時，就可用卡瓦列里原理求出另一個圖形的面積或體積。

利用不可分量方法，卡瓦列里解決的典型問題是有關平行四邊形中線段和組成它的三角形中的線段關係的一些定理．它們對後來的數學發展產生了深遠的影響．一個基本的命題是：設平行四邊形ACDF(如圖2)被對角線CF分成兩個三角形ACF和DCF，則平行四邊形(面積)是每個三角形(面積)的兩倍．卡瓦列里這樣證明：先作EF=CB，再作HE∥CD，BM∥CD，則HE=BM，則△ACF中所有線段與△DCF中所有線段對應相等，從而兩個三角形相等，因而平行四邊形ACDF中所有線段之和等於每個三角形中的和的兩倍．用類似的但有更大難度的方法，卡瓦列里進一步證明了平行四邊形內線段平方的和等於每個三角形內線段平方和的三倍．利用這一命題，易證圓錐的體積是其外接圓柱體積的三分之一，拋物線弓形是其外接矩形面積的三分之二等．這些都是阿基米德已得出的結果，但卡瓦列里採用統一的方法來處理，不僅使許多利用窮竭法勉強解決的問題，到來21世紀可以很方便地求解，如橢圓面積和球體積等，而且使認識深化，得出了更深刻的結果．卡瓦列里沿處理構成平行四邊形的線段的冪和組成平行四邊形的三角形內相應線段的冪的比，不斷前進：他已求出兩組線段之和的比為2∶1；線段平方和之比為3∶1；接著又求出兩組線段立方和之比為4∶1；4次冪和之比為5∶1(在此基礎上他求出拋物線弓形繞其弦旋轉而成的立體的體積)；線段的5次冪和之比為6∶1；6次冪和之比為7∶1等等；最後，兩組線段的n次冪和之比為(n+1)∶1．即得出

按他的平面圖形由線段構成的思想，Σa表示一個以a為邊長的正方形的面積；類似地，Σa2表示一個以Σa為截面(以a為邊長)的正方體的體積，因而有

並驗證了n=5，6，…，9的情況，n=1，2的情況已為阿基米德所證明，阿拉伯人已知n=4的情況．卡瓦列里的工作是前人工作的推廣和統一化．雖然在卡瓦列里之前，費馬和羅貝瓦爾用別的方法也得到了這一結果，但1639年他第一個公開發表了這一公式，對17世紀無窮小分析的發展起了重要的推動作用．可以說這是在無窮小分析中指出更一般的代數運演演算法則的可能性的第一個定理．後來由牛頓和萊布尼茨提出而成為積分學的基礎．

由此公式出發，卡瓦列里立即證明了在單位區間上，曲線y=xn(n為正整數)下的圖形面積為

這個圖形圍繞“弦”旋轉而成的立體體積為

卡瓦列里極大地推進了不可分量方法，不僅把它視為發現的方法，也試圖使它成為證明的方法．這樣一來，就必須按數學證明的基本要求，使概念嚴格化，即產生了這樣一個問題：不可分量究竟是什麼？

卡瓦列里了解這一問題的複雜性，因而想建立一種獨立於數學基本要求的方法，使得無論概念是怎樣形成的，這種方法都是有效的．他甚至認為，嚴格性是哲學的事，而不是幾何學的事．卡瓦列里沒有肯定連續量可以分解為他並沒有給出明確定義的不可分的元素，他也沒有講清楚它們究竟是實在的還是潛在的無窮小量．

卡瓦列里從未解釋過沒有厚薄的不可分量是怎樣構成面積和體積的，但在許多場合，他曾把不可分量方法和運動的觀點聯繫起來，認為面積和體積可以看作是由不可分量的運動產生出來的．不過他並沒有將這種有啟發性的觀點發展成為幾何方法，這一點為他的後繼者托里切利所實現，結果產生了牛頓的流數法．卡瓦列里的不可分量在沃利斯的《無窮算術》中有所應用，在牛頓和萊布尼茨的數學思想中也有所反映，如前者的“瞬”概念和後者的“微分”概念中就有不可分量的影子．卡瓦列里的思想，對微積分的發展起了巨大的啟發作用．

當然卡瓦列里的不可分量方法與微積分尚有較大的距離，主要表現在：(1)沒有極限概念；(2)沒有採用代數或算術方法，而它們是定義微積分的前提之一；(3)過於強調面積和體積的比而不是直接求積．與阿基米德相比，卡瓦列里在求積方法的統一性上邁出了決定性的一步；與牛頓、萊布尼茨相比，卡瓦列里可以說是他們的直接前驅之一．因而，卡瓦列里的工作是由古希臘人的方法向現代微積分過渡的一個不可缺少的環節．正如萊布尼茨在給曼弗雷迪的一封信中所說：“幾何學中的卓越人物、完成了這一領域中義勇軍任務的開拓者和倡導者是卡瓦利里和托里切利，後來別人的進一步發展部得益於他們的工作。”

圖不可分量方法中學數學試驗教材

卡瓦列利運用上述定理求得了許多平面圖形的面積和立體圖形的體積，其中包括球體積。中學數學試驗教材之前的很長時間裡，我國的立體幾何教材一直採用卡瓦列利的方法來推導球體積公式。

事實上，中國古代著名數學家祖沖之、祖暅父子就提出“冪勢既同，則積不容異。”即“等高處截面面積相等，則二立體的體積相等。”的定理，並由此嚴格推導出球體體積的計算公式。祖氏父子對該原理的發現和運用要比卡瓦列利早一千年。故又被稱為“祖暅原理”。