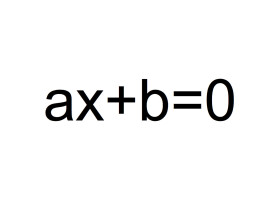一元一次方程
數學中的整式方程、線性方程
一元一次方程指只含有一個未知數、未知數的最高次數為1且兩邊都為整式的等式。一元一次方程只有一個根。
一元一次方程最早見於約公元前1600年的古埃及時期。公元820年左右，數學家花拉子米在《對消與還原》一書中提出了“合併同類項”、“移項”的一元一次方程思想。16世紀，數學家韋達創立符號代數之後，提出了方程的移項與同除命題。1859年，數學家李善蘭正式將這類等式譯為一元一次方程。
一元一次方程最早見於約公元前1600年的古埃及時期。
一元一次方程
公元前1世紀左右，中國人在《九章算術》中首次加入了負數，並提出了正負數的運演演算法則，解決了移項問題。在“盈不足”一章中提出了盈不足術。但該方法並沒有被用來解決一元一次方程。在11～13世紀時傳入阿拉伯地區，並被稱為“契丹演演算法”。
9世紀，阿拉伯數學家花拉子米在《對消與還原》中給出了解方程的簡單可行的基本方法，即“還原”和“對消”。但沒有採用字母符號。體現了明顯的方程的思想。
12世紀，印度數學家婆什迦羅在《麗拉沃蒂》一書中用假設法（設未知數）來解決一類一元一次方程。由於所假設的數可以是任意正數，婆什迦羅稱上述方法為“任意數演演算法”。
一元一次方程
16世紀時，明代數學家程大位（1533-1606）在《演演算法統宗》一書中也用假設法來解一元一次方程。
1859年，中國數學家李善蘭正式將這類等式譯為一元一次方程。
只含有一個未知數，且未知數的高次數是1，等號兩面都是整式，這樣的方程叫做一元一次方程（linear equation with one unknown）。其一般形式是：
有時也寫作：
可以通過等式性質化簡而成為一元一次方程的整式方程（如）也屬於一元一次方程。一元一次方程是一種線性方程，且只有一個根。
解一元一次方程有五步，即去分母、去括弧、移項、合併同類項、係數化為1，所有步驟都根據整式和等式的性質進行。
以解方程為例：
去分母，得：
去括弧，得：
移項，得：
合併同類項，得：（常簡寫為“合併，得：”）
係數化為1，得：在一元一次方程中，去分母一步通常乘以各分母的最小公倍數，如果分母為分數，則可化為該一項的其他部分乘以分母上分數的倒數的形式。
以方程為例：
消除分母上的分數，可化簡為：進而得出方程的解。
如果分母上有無理數，則需要先將分母有理化。
基本公式
對於關於x的一元一次方程，其求根公式為：
推導過程
解：移項，得：
係數化為1，得：
一元一次方程
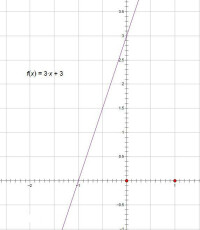
以方程為例：
如圖，作出函數的圖象。
∵函數圖象與x軸交於點
∴原方程的根是
一元一次方程通常可用於做數學應用題。也可應用於物理、化學的計算，如給出液體密度和壓強，通過公式計算液體深度的問題。
丟番圖問題
希臘數學家丟番圖的墓碑上記載著：他生命的六分之一是幸福的童年；再活了他生命的十二分之一，兩側長起長長的鬍子；他結了婚，又度過了一生的七分之一；再過五年，他有了兒子，感到很幸福；可是兒子只活了他父親全部年齡的一半；兒子死後，他再極度悲痛中度過了四年，也與世長辭了。根據以上信息，算出：（1）丟番圖的壽命；（2）丟番圖開始當爸爸時的年齡；（3）兒子死時丟番圖的年齡。
解法：設丟番圖的壽命x歲；
則
解得x=84,
∴丟番圖開始當爸爸時的年齡：
兒子死時丟番圖的年齡：84-4=80
雞兔同籠問題
“雞兔同籠問題”是我國古算書《孫子算經》中的數學問題，其內容是：“今有雉（雞）兔同籠，上有三十五頭，下有九十四足。問雉兔各幾何。”譯成現代漢語為：有若干只雞和兔在同個籠子里，從上面數，有三十五個頭；從下面數，有九十四隻腳。籠中各有幾隻雞和兔？
該問題可用一元一次方程解決，解法如下：
解法：設雞有x只，兔有隻
由題意得：
解得：x=23
∴35-x=12
答：雞有23隻，兔有12隻。
有限循環小數化為分數問題
利用一元一次方程可以將一個有限循環小數化為分數，以為例：
設，則
可算出
同時，該方法也可用來證明的問題。
一元一次方程可以解決絕大多數的工程問題、行程問題、分配問題、盈虧問題、積分表問題、電話計費問題、數字問題。如果僅使用算術，部分問題解決起來可能異常複雜，難以理解。而一元一次方程模型的建立，將能從實際問題中尋找等量關係，抽象成一元一次方程可解決的數學問題，通過驗證一元一次方程解的合理性，達到解釋和解決生活問題的目的，從一定程度上解決了一部分生產、生活中的問題。
基本信息
- 中文名
- 一元一次方程
- 外文名
- linear equation with one unknown
- 求解公式
- x=-b/a
- 標準形式
- ax+b=0或ax=b（a≠0）
- 類型
- 整式方程、線性方程
- 學科
- 數學
- 創立者
- 韋達