估計理論
估計理論
目錄
應用統計學方法來研究,用接收到的有雜訊的觀測數據估計實際參量或隨機變數、隨機過程或系統某些特性的理論,為資訊理論的一個分支。估計分為參量估計和狀態估計兩類。參量和狀態的區別是:前者隨著時間保持不變或只緩慢變化;後者則隨著時間連續變化。例如,根據雷達回波來估計每一時刻在連續變化的衛星的三個空間位置矢量和三個速度矢量,這是狀態估計。對衛星的質量和慣量等的估計則屬於參量估計。被估計的參量又可分為隨機變數和非隨機變數兩種。要估計的狀態則又有離散時間和連續時間的區別。
發展概況 19世紀初,德國數學家C.F.高斯提出了最小二乘法估計(最小平方誤差估計)。從20世紀20年代到30年代,英國統計學家R.A.費歇耳系統地建立了經典估計理論。1941年蘇聯科學家H.柯爾莫戈洛夫首先論述離散時間情況下的預測問題。美國科學家N.維納於1942年推導出連續時間濾波。他們都把統計方法應用於解決與狀態估計有關的最佳線性濾波問題,為現代估計理論奠定了基礎。60年代初,R.E.卡爾曼等人發展了維納理論,把狀態變數法引入濾波理論,用時域微分方程表示濾波問題,得到遞歸濾波演演算法,適於用計算機求解和實時處理。這一突破使估計理論在許多領域得到實際應用。80年代初,光纖通信和激光雷達等逐漸成為工程現實,量子通道與量子檢測和估計理論遂引起人們的注意。
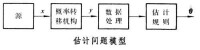
估計理論
估計理論
估計理論
估計理論
如果的期望值為零,即
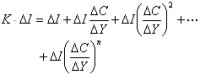
估計理論
估計理論
估計理論
估計理論
估計理論
則 稱為一致估計。
稱為一致估計。
估計理論
① 最小平方誤差估計:對信號和雜訊的統計知識可以不作任何要求。它的基本點是使 n次觀測值與理論計算值的絕對誤差在平方和意義下最小,並由此求得估計量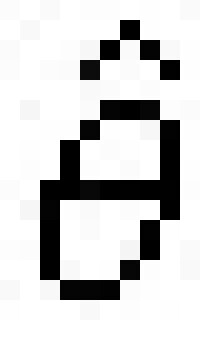 。若u是變數x,y,…的函數並含有m個參量θ1,θ2,…,θm,即
。若u是變數x,y,…的函數並含有m個參量θ1,θ2,…,θm,即
估計理論
u=f(θ1,θ2,…,θm;x,y,…)
對u和x,y,…作n次觀測,得
(xi,yi,…,ui) (i=1,2,…,n)
於是u的理論計算值 與觀測值ui的絕對誤差為,i=1,2,…,n。如n個絕對誤差的平方和最小,從而使函數u與觀測值u1,u2,…,un最佳擬合,也就是使參量θ1,θ2,…,θm滿足下列關係
與觀測值ui的絕對誤差為,i=1,2,…,n。如n個絕對誤差的平方和最小,從而使函數u與觀測值u1,u2,…,un最佳擬合,也就是使參量θ1,θ2,…,θm滿足下列關係
估計理論
媉θ/媉θi=0 (i=1,2,…,m)
由此可求得最小平方誤差估計量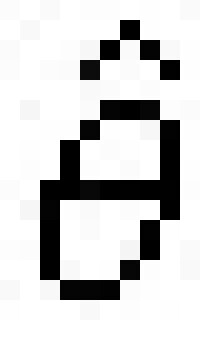 1,
1,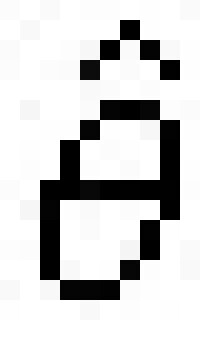 2,…,
2,…,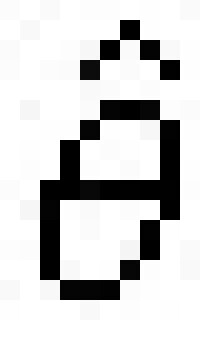 m。
m。
估計理論
估計理論
估計理論
②極大似然估計:以似然函數的概念為基礎。用Y表示一組觀測量,θ表示一組未知參量,則條件密度函數p(Y|θ)是Y 和θ兩者的函數。如果規定Y等於其觀測量Y*,則p(Y*│θ只是θ的函數,並稱為似然函數。其涵義是似然函數p(Y*|θ)的值越大,則θ是準確值的可能性也越大。使p(Y*θ)最大的θ就是極大似然估計量,通常用表示。
③貝葉斯估計:對於單參量估計(多參量估計的情況相似)來說,首先要給定隨機參量 θ的概率密度函數p(θ)和因估計誤差而帶來的代價函數C(θ,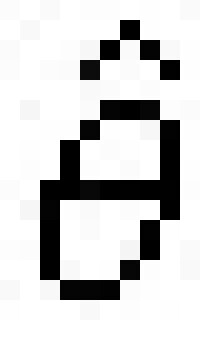 )。假設處理裝置對Y進行了n次測量,y=(y1,y2,…,yn),且已知θ時y的條件聯合概率密度為p(y│θ),則估計量
)。假設處理裝置對Y進行了n次測量,y=(y1,y2,…,yn),且已知θ時y的條件聯合概率密度為p(y│θ),則估計量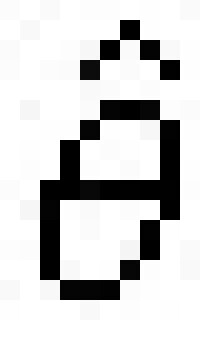 (y)帶來的風險為
(y)帶來的風險為
估計理論
估計理論
平均風險為
貝葉斯估計就是使平均風險R(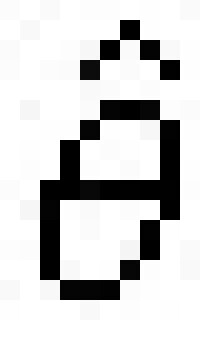 )成為最小的估計。可由方程
)成為最小的估計。可由方程
估計理論
解出貝葉斯估計量。
參考書目
H. L. Van Trees, Detection, Estimation and Modulation Theory, Part I, John Wiley,New York,1968.