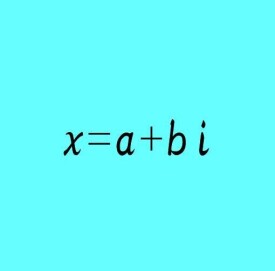虛根
方程的複數根
【imaginary root】包括虛數單位的方程的根，亦即有負數平方根的方程的根。
定理一
如果實數係數方程有虛根，這裡a和b都是實數，那麼它還有另一個虛根。
因為實數係數方程如果有虛根，共軛虛根一定成對出現，所以我們可以得出下面的兩個推論。
推論1
實數係數奇次方程至少有一個實根，一般有奇數個實根。
推論2
實數係數偶次方程或者沒有實根，或者有偶數個實根。
因為實數係數方程有一個實根c，就有一個實數係數因式和它對應，有一對虛根，就有一個實數係數因式和它對應，所以我們又可以得出下面的推論。
推論3
實數係數多項式一定是一次或者二次的實數係數不可約因式的積。
定理2
定理3
如果有理數係數方程有無理根，這裡a、b、c和d是有理數，是無理數，ab≠0，那麼它還有另外三個無理根，和。
定理4
如果有理數係數方程有一個根是，這裡a、b和c是有理數，是無理數，，那麼它還有另外三個根，和。
定理5
如果有理數係數方程有一個根是，這裡a、b、c和d是有理數，是無理數，那麼它還有另外三個根。
基本信息
- 中文名
- 虛根
- 外文名
- imaginary root
- 相關概念
- 共軛虛根、複數等
- 定義
- 方程的複數根