向量線
向量線
向量線(vector line)是向量場中具有特定意義的曲線,指其切線方向與場中向量一致的向量場中的曲線。設f是定義在區域Ω⊆R上的向量場,Γ是Ω中的光滑曲線,若Γ上每一點處的切向量的方向與f在該點的方向一致,則Γ稱為場f的向量線。例如勢場f的向量線是它的勢函數的梯度線,即這個勢函數變化最快的線。若f是穩定流動(即與時間無關)的流體的速度場,則它的向量線是流體質點的移動軌跡,稱為流線,若f是引力場,則相應的向量線稱為力線。
我們知道,在穩定流動的流體中,質點的瞬時運動方向是該點的速度方向,這就是說,流體中質點的運動軌跡的切線方向,就是速度方向,這條軌跡稱為 流線。這就是一般向量場中的 向量線概念。
設
向量線
向量線
向量線
向量線
向量線
向量線
向量線
向量線
向量線
向量線
向量線
就是向量線在點處的切向量。由定義,它與在點處的場向量共線,因此
向量線
向量線
向量線
這就是向量線所滿足的方程,如果解出它的話,一般就得到 向量線族。如果再利用過點這個條件,就得到過點的向量線。一般來說,向量場中每一點有一條且僅有一條向量線通過它,向量線族充滿了向量場所在的空間。
向量線
向量線
向量線
向量線
向量線
其中為點到原點的距離,,為真空介電常數。
將E具體寫出來就是
向量線
向量線
向量線
向量線
所以
向量線
向量線
向量線
向量線
2. 設為任意一張光滑或分片光滑的封閉曲面。
向量線
向量線
向量線
(i) 如果內不含原點。記所包圍的區域為,則由Gauss公式得
向量線
向量線
向量線
向量線
向量線
向量線
向量線
(ii) 如果內含有原點,那麼不能直接用Gauss公式。在曲面所包圍的區域內取一個以原點為心的小球面,定向取內側。記為介於與之間的區域。由Gauss 公式得
向量線
向量線
因此從內部穿出曲面的電通量
向量線
向量線
因此,電場強度穿出任一封閉曲面的電通量等於其內部的電荷量除以,這正是電磁學中的 Gauss定律。
此外,利用前面的討論,電場強度的向量線(即電力線)應滿足關係式
向量線
向量線
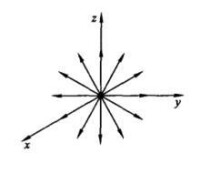
圖1
